Tutorial walkthrough

Having outlined on the previous page some of the big-picture story—how meep_adjoint fits into the larger design-optimization ecosystem, and what you can expect to put into and get out of a typical session—on this page we get down to details. We will present a step-by-step walkthrough of a meep_adjoint session that, starting from scratch, automagically finds intricate and highly non-intuitive device designs whose performance far exceeds anything we could hope to design by hand.

The problem: optimal routing of optical power flows

The engineering problem we will be considering is the design of interconnect router devices for optical networks. For our purposes, a router is a hunk of lossless dielectric material, confined within a rectangular (2D) or box-shaped (3D) region of given fixed dimensions, from which emanate four stub waveguides (of given fixed sizes and materials) representing I/O ports, which we label simply East, West, North, and South.

The router will live inside an optical-network switch with each port connected to a fiber-optic cable carrying incoming and outgoing signals, and our job is to design the central hub to ensure that signals arriving on some given set of input ports are routed to some given set of output ports with optimality according to some given set of desiderata. Evidently, different choices of input and output ports and performance criteria yield different optimization problems, and we will show how this freedom is reflected in the meep_adjoint API and our python driver scripts. For most this tutorial, we will focus on two particular design tasks:

  • Right-angle router: Steer incoming signals arriving on the West port through a 90-degree bend to depart via the North port. Here the design objective is simply to maximize transfer of signal power from input to output, minimizing losses due to leakage power emissions from the South or East ports.

  • Three-way splitter: Split an input signal arriving on the West port into three equal-power output signals departing via the North, South, and East ports. For this task we will suppose that the design objective is not maximum output power, but rather maximal uniformity of power emissions from the three output ports.

The driver script: router.py

The driver script for this problem is router.py, which lives in the examples subdirectory of the meep_adjoint source distribution. Click below for a sneak peak at this script, or read on for a step-by-step discussion.

File: examples/router.py (Click to show/hide) 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
import sys
import os
import argparse

import numpy as np
import meep as mp

import meep_adjoint
from meep_adjoint import get_adjoint_option as adj_opt
from meep_adjoint import get_visualization_option as vis_opt

from meep_adjoint import ( OptimizationProblem, Subregion,
                           ORIGIN, XHAT, YHAT, ZHAT, E_CPTS, H_CPTS, v3, V3)

######################################################################
# subroutine that initializes and returns an OptimizationProblem
# structure for the router geometry
######################################################################
def init_problem():
    """ Initialize four-way router optimization problem.

    Args:
        None (reads command-line options from sys.argv).

    Returns:
        New instance of meep_adjoint.OptimizationProblem()
    """

    ######################################################################
    # set custom defaults for meep_adjoint package-wide options, then
    # fetch values for a few such options we will need in this routine
    ######################################################################
    meep_adjoint.set_option_defaults( { 'fcen': 0.5, 'df': 0.2,
                                        'dpml': 1.0, 'dair': 0.5,
                                        'eps_design': 6.0
                                      })
    fcen = adj_opt('fcen')
    dpml = adj_opt('dpml')
    dair = adj_opt('dair')

    ######################################################################
    # process script-specific command-line arguments...
    ######################################################################
    parser = argparse.ArgumentParser()

    # options affecting the geometry of the router
    parser.add_argument('--w_east',   type=float, default=1.5,  help='width of EAST waveguide stub')
    parser.add_argument('--w_west',   type=float, default=1.5,  help='width of WEST waveguide stub')
    parser.add_argument('--w_north',  type=float, default=1.5,  help='width of NORTH waveguide stub')
    parser.add_argument('--w_south',  type=float, default=1.5,  help='width of SOUTH waveguide stub')
    parser.add_argument('--l_stub',   type=float, default=3.0,  help='waveguide stub length')
    parser.add_argument('--l_design', type=float, default=4.0,  help='design region side length')
    parser.add_argument('--h',        type=float, default=0.0,  help='thickness in z-direction')
    parser.add_argument('--eps_wvg',  type=float, default=6.0,  help='waveguide permittivity')

    parser.add_argument('--full_dft', action='store_true', help='tabulate and plot fields over full computational cell')

    # options affecting the type of device to design
    parser.add_argument('--splitter', action='store_true', help='design equal splitter instead of right-angle router')

    args = parser.parse_args()

    w_east   = args.w_east
    w_west   = args.w_west
    w_north  = args.w_north
    w_south  = args.w_south
    l_stub   = args.l_stub
    l_design = args.l_design
    h        = args.h
    eps_wvg  = args.eps_wvg
    splitter = args.splitter

    ##################################################
    # set up optimization problem
    ##################################################

    #----------------------------------------
    # computational cell
    #----------------------------------------
    lcen          = 1.0/fcen
    dpml          = 0.5*lcen if dpml==-1.0 else dpml
    sx = sy       = dpml + l_stub + l_design + l_stub + dpml
    sz            = 0.0 if h==0.0 else (dpml + dair + h + dair + dpml)
    d_flux        = 0.5*(l_design + l_stub)     # distance from origin to NSEW flux monitors
    d_flx2        = d_flux + l_stub/3.0         # distance from origin to west2 flux monitor
    d_source      = d_flux + l_stub/6.0         # distance from origin to source
    cell_size     = [sx, sy, sz]

    #----------------------------------------------------------------------
    #- geometric objects (material bodies), not including the design object
    #----------------------------------------------------------------------
    wvg_mat    = mp.Medium(epsilon=eps_wvg)
    east_wvg   = mp.Block(center=V3(ORIGIN+0.25*sx*XHAT), material=wvg_mat, size=V3(0.5*sx, w_east,  h) )
    west_wvg   = mp.Block(center=V3(ORIGIN-0.25*sx*XHAT), material=wvg_mat, size=V3(0.5*sx, w_west,  h) )
    north_wvg  = mp.Block(center=V3(ORIGIN+0.25*sy*YHAT), material=wvg_mat, size=V3(w_north, 0.5*sy, h) )
    south_wvg  = mp.Block(center=V3(ORIGIN-0.25*sy*YHAT), material=wvg_mat, size=V3(w_south, 0.5*sy, h) )

    background_geometry = [ east_wvg, west_wvg, north_wvg, south_wvg ]

    #----------------------------------------------------------------------
    # source region
    #----------------------------------------------------------------------
    source_center  = ORIGIN - d_source*XHAT
    source_size    = 2.0*w_west*YHAT
    source_region  = Subregion(center=source_center, size=source_size, name=mp.X)

    #----------------------------------------------------------------------
    #- design region
    #----------------------------------------------------------------------
    design_center = ORIGIN
    design_size   = [l_design, l_design, h]
    design_region = Subregion(name='design', center=design_center, size=design_size)

    #----------------------------------------------------------------------
    #- objective regions
    #----------------------------------------------------------------------
    n_center   = ORIGIN + d_flux*YHAT
    s_center   = ORIGIN - d_flux*YHAT
    e_center   = ORIGIN + d_flux*XHAT
    w1_center  = ORIGIN - d_flux*XHAT
    w2_center  = w1_center - (l_stub/3.0)*XHAT

    north      = Subregion(center=n_center,  size=2.0*w_north*XHAT, dir=mp.Y,  name='north')
    south      = Subregion(center=s_center,  size=2.0*w_south*XHAT, dir=mp.Y,  name='south')
    east       = Subregion(center=e_center,  size=2.0*w_east*YHAT,  dir=mp.X,  name='east')
    west1      = Subregion(center=w1_center, size=2.0*w_west*YHAT,  dir=mp.X,  name='west1')
    west2      = Subregion(center=w2_center, size=2.0*w_west*YHAT,  dir=mp.X,  name='west2')

    objective_regions = [north, south, east, west1, west2]

    #----------------------------------------------------------------------
    # objective function and extra objective quantities -------------------
    #----------------------------------------------------------------------
    fobj_router   = '|P1_north|^2'
    fobj_splitter = '( |P1_north| - |P1_east| )^2 + ( |P1_east| - |M1_south| )^2'
    objective_function = fobj_splitter if splitter else fobj_router
    extra_quantities = ['S_north', 'S_south', 'S_east', 'S_west1', 'S_west2']

    #----------------------------------------------------------------------
    #- optional extra regions for visualization
    #----------------------------------------------------------------------
    full_region = Subregion(name='full', center=ORIGIN, size=cell_size)
    extra_regions = [full_region] if args.full_dft else []

    #----------------------------------------------------------------------
    #----------------------------------------------------------------------
    #----------------------------------------------------------------------
    return OptimizationProblem(
     cell_size=cell_size,
     background_geometry=background_geometry,
     source_region=source_region,
     objective_regions=objective_regions,
     design_region=design_region,
     extra_regions=extra_regions,
     objective_function=objective_function,
     extra_quantities=extra_quantities
    )


######################################################################
######################################################################
######################################################################
if __name__ == '__main__':

    opt_prob = init_problem()

The phases of a meep_adjoint session and the structure of this tutorial

This tutorial consists of three parts, corresponding to the three stages of a typical meep_adjoint session:

1. Initialization: Defining the problem and initializing the solver

The first step is to identify all of the ingredients needed to define our design-optimization problem and communicate them to meep_adjoint in the form of arguments passed to the OptimizationProblem constructor. The class instance we get back will furnish the portal through which we access meep_adjoint functionality and the database that tracks the evolution of our design and its performance.

The initialization phase also typically involves setting appropriate customized values for the many configuration options affecting the behavior of meep_adjoint.


2. Interactive exploration: Single-point calculations and visualization

Before initiating a lengthy, opaque machine-driven design iteration, we will first do some human-driven poking and prodding to kick the tires of our OptimizationProblem—both to make sure we defined the problem correctly, and also to get a feel for how challenging it seems, which will inform our choice of convergence criteria and other parameter settings for the automated phase. More specifically, in this phase we will invoke meep_adjoint API routines to do the following:

  1. update the design function \(\epsilon^\text{des}(\mathbf{x})\)—that is, move to a new point \(\boldsymbol{\beta}\) in design space

  2. numerically evaluate the objective-function value \(f^\text{obj}(\boldsymbol{\beta})\) at the current design point

  3. numerically evaluate the objective-function gradient \(\boldsymbol{\nabla} f^\text{obj}\) at the current design point

  4. produce graphical visualizations of both the device geometry—showing the spatially-varying permittivity distribution of the current design—and the results of the meep calculations of the previous two items, showing the spatial configuration of electromagnetic fields produced by the current iteration of the device design.

Because steps B, C, and D here are executed with the device design held fixed at a single point in design space, we refer to them as static or single-point operations, to be distinguished from the dynamic multi-point trajectory through design space traversed by the automated design optimization of the following stage.

Of course, of all the single-point tests we might run in our interactive investigation, perhaps the most useful is

  1. check the adjoint calculation of step C above by slightly displacing the design point in the direction of the gradient reported by meep_adjoint and confirming that this does, in fact, improve the value of the objective function—that is, compute \(f^\text{obj}\Big(\boldsymbol{\beta} + \alpha\boldsymbol{\nabla} f\Big)\) (with \(\alpha\sim 10^{-2}\) a small scalar value) and verify that it is an improvement over the result of step B above.


3. Automation: Machine-driven iterative design optimization

Once we’ve confirmed that our problem setup is correct and acquired some feel for how it behaves in practice, we’ll be ready to hand it off to a numerical optimizer and hope for the best. As we will demonstrate, the easiest way to proceed here is to invoke the simple built-in gradient-descent optimizer provided by meep_adjoint—which, we will see, is more than adequate to yield excellent results for the specific problems addressed in this tutorial—but we will also show how, with only slightly more effort, you can use your favorite external gradient-based optimization package instead.

Phase 1: Problem definition and initialization:
Creating an OptimizationProblem

The first step in every meep_adjoint workflow is to create an instance of OptimizationProblem. This class plays for meep_adjoint a role analogous to that of the Simulation class in the core meep python module : its public methods offer access to the computational capabilities of the solver, and its internal data fields keep track of all data and state needed to track the progress of a computational session.

The OptimizationProblem constructor accepts a large number of required and optional input arguments, whose setup will typically occupy a straightforward but somewhat lengthy chunk of your driver script. You will find detailed auto-generated documentation for the full set of arguments in the API reference, but in most cases you’ll probably be able simply to copy the initialization code from router.py or one of the other worked examples and modify as appropriate for your problem.

The next section offers a quick list of the most important constructor arguments (again deferring the exhaustive documentation to the API reference), and the following section illustrates their use in practice via an annotated walkthrough of the router.py initialization code.

Roughly speaking, the inputs needed to instantiate an OptimizationProblem may be grouped into three categories (click the title headers below to expand/collapse content):

Parameters describing the underlying FDTD simulation geometry

cell_size

List or numpy array of computational cell dimensions, identical to the parameter of the same name passed to the Simulation constructor.

background_geometry

foreground_geometry

List of GeometricObject structures describing material bodies in the geometry, not including the design region, for which meep_adjoint automatically creates an appropriate object internally. The “background” and “foreground” lists contain objects that logically lie “beneath” and “above” the design region; internally, these lists are concatenated, with the automatically-created design object in between, to form the list of objects passed as the geometry input to the Simulation constructor

sources

List of Source structures describing excitation sources, passed without modification as the parameter of the same name to the Simulation constructor. 1

source_region

This is a convenience argument that may be used instead of sources for problems with only a single excitation source. If present, source_region should be a Subregion (or a Volume) specifying the spatial extent of the source, which meep_adjoint will use together with the values of configuration options 2 to construct a single-element list passed as the sources parameter to the Simulation constructor.

Parameters describing the objective function and how it is computed

objective_regions

List of Subregion structures for all objective region. (A Subregion in meep_adjoint is basically just what would be a FluxRegion or EnergyRegion or another similar structure in meep , except that each Subregion has a unique name, such as north or east for flux monitors on the various I/O ports of the router geometry.)

objective_function

Character string specifying a mathematical expression involving one or more objective quantities.

extra_quantities

An optional list of additional objective quantities for which to compute and report values in addition to the objective function and the objective quantities needed to compute it.

Parameters describing the design space and the tweakable degrees of freedom

design_region

Subregion (or Volume) specifying the design region.

basis

Instance of Basis describing the space of design permittivity functions.

In router.py, the setup and initialization code lives in a function called init_problem, which accepts no arguments and returns a new instance of OptimizationProblem, referring both to router.py-specific command-line arguments and meep_adjoint-wide configuration options for various pieces of information. What follows is a detailed walk through this routine with a blow-by-blow analysis of the various initialization tasks it handles.

1A. Fetch values for global (meep-adjoint-wide) and local (script-specific) and configurable options

Like most meep_adjoint driver scripts, router.py makes use of user-configured settings for both general-purpose (problem-independent) configuration options defined by meep_adjoint and problem-specific options defined by router.py.

Examples of the former include the options fcen (center frequency of forward sources), dpml (thickness of PML layers), and dair (thickness of air gaps between material bodies and PML layers) In lines 37-39 below we query meep_adjoint for its current values of those options (note that adj_opt is short for meep_adjoint.get_adjoint_option).

Just before this, in lines 33-36, we call set_option_defaults to update some of the hard-coded default option values in meep_adjoint to values that make more sense for the router problem. Note that this step only affects the default option settings, which are still overridden by command-line arguments or configuration files. For more on this, see the configuration section of this documentation tree.

 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
     import meep as mp
     import meep_adjoint
     from meep_adjoint import get_adjoint_option as adj_opt
     from meep_adjoint import get_visualization_option as vis_opt

     from meep_adjoint import ( OptimizationProblem, Subregion,
                                ORIGIN, XHAT, YHAT, ZHAT, E_CPTS, H_CPTS, v3, V3)

     ######################################################################
     # subroutine that initializes and returns an OptimizationProblem
     # structure for the router geometry
     ######################################################################
     def init_problem():
         """ Initialize four-way router optimization problem.

         Args:
             None (reads command-line options from sys.argv).

         Returns:
             New instance of meep_adjoint.OptimizationProblem()
         """

         ######################################################################
         # set custom defaults for meep_adjoint package-wide options, then
         # fetch values for a few such options we will need in this routine
         ######################################################################
         meep_adjoint.set_option_defaults( { 'fcen': 0.5, 'df': 0.2,
                                             'dpml': 1.0, 'dair': 0.5,
                                             'eps_design': 6.0
                                           })
         fcen = adj_opt('fcen')
         dpml = adj_opt('dpml')
         dair = adj_opt('dair')

Then (lines 45-71) we follow the usual argparse procedure to define a number of options specific to the router geometry—such as the widths or permittivity of the waveguides—and parse router.py command-line arguments for their settings.

45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
 parser = argparse.ArgumentParser()

 # options affecting the geometry of the router
 parser.add_argument('--w_east',   type=float, default=1.5,  help='width of EAST waveguide stub')
 parser.add_argument('--w_west',   type=float, default=1.5,  help='width of WEST waveguide stub')
 parser.add_argument('--w_north',  type=float, default=1.5,  help='width of NORTH waveguide stub')
 parser.add_argument('--w_south',  type=float, default=1.5,  help='width of SOUTH waveguide stub')
 parser.add_argument('--l_stub',   type=float, default=3.0,  help='waveguide stub length')
 parser.add_argument('--l_design', type=float, default=4.0,  help='design region side length')
 parser.add_argument('--h',        type=float, default=0.0,  help='thickness in z-direction')
 parser.add_argument('--eps_wvg',  type=float, default=6.0,  help='waveguide permittivity')

 # options affecting the type of device to design
 parser.add_argument('--splitter', action='store_true', help='design equal splitter instead of right-angle router')

 args = parser.parse_args()

 w_east   = args.w_east
 w_west   = args.w_west
 w_north  = args.w_north
 w_south  = args.w_south
 l_stub   = args.l_stub
 l_design = args.l_design
 h        = args.h
 eps_wvg  = args.eps_wvg
 splitter = args.splitter

Mining command-line options for global and local options

Note that the command-line options to router.py may be used to specify values for both meep_adjoint options (like fcen) and for router.py options (like w_south). How do the two sets of options, parsed at different times by separate parsers in distinct modules, coexist on the router.py command line?

Answer: meep_adjoint takes a first crack at sys.argv, handling and removing all arguments it understands, and leaving arguments it doesn’t recognize untouched in their original sequence within sys.argv. (It uses Argparser.parse_known_args instead of parse_args) This happens when meep_adjoint initializes its databases of user-configurable options, which it does on a just-in-time basis the first time an option value is queried; in the present case, that happens on line 36, well before router.py takes its own crack at sys.argv (on line 60).

One difference between meep_adjoint configuration options and router.py commmand-line options is that the former may also be set in configuration files. See the customization section of this documentation for more information.

1B. Set up the computational cell and the fixed geometry

The next steps are standard initialization procedures familiar to anyone who has ever initialized a Simulation . First we do a little arithmetic to compute the dimensions of the computational cell based on the current values of user-configurable geometric parameters like design_length (the side length of the central square hub region we are trying to design) and dpml (thickness of PML layers):

81
82
83
84
85
86
lcen          = 1.0/fcen
dpml          = 0.5*lcen if dpml==-1.0 else dpml
design_length = args.l_design
sx = sy       = dpml + l_stub + design_length + l_stub + dpml
sz            = 0.0 if h==0.0 else dpml + dair + h + dair + dpml
cell_size     = [sx, sy, sz]

Problem-specific vs. package-wide configuration options

Note that some of the user-configurable geometric parameters we reference here—such as design_length and l_stub (length of stub waveguide sections)—are router.py-specific command-line options, while others—such as dpml and dair (length of air gaps between device outer perimeter and PML layers) are meep_adjoint configuration options. This is not because PML thicknesses or air gaps play particularly special roles in adjoint calculations, but simply because pretty much every conceivable FDTD project will want to define user-configurable options for these quantities, so meep_adjoint just defines them once and for all at the package level, obviating the need for users to define e.g. a dpml parameter in every meep_adjoint script they write.

Next we construct a list of GeometricObject structures to describe the fixed portion of the material geometry—that is, everything except for the design region in which we are allowed to tweak the permittivity This is just like the list of objects one constructs and passes as the geometry parameter to the Simulation constructor in the core meep python module , except that in forming this list we need only account for material bodies lying outside the design region; the material geometry inside the design region is handled entirely internally within meep_adjoint, and our only responsibility is to tell the OptimizationProblem constructor where the design region is via the design_region parameter (see below).

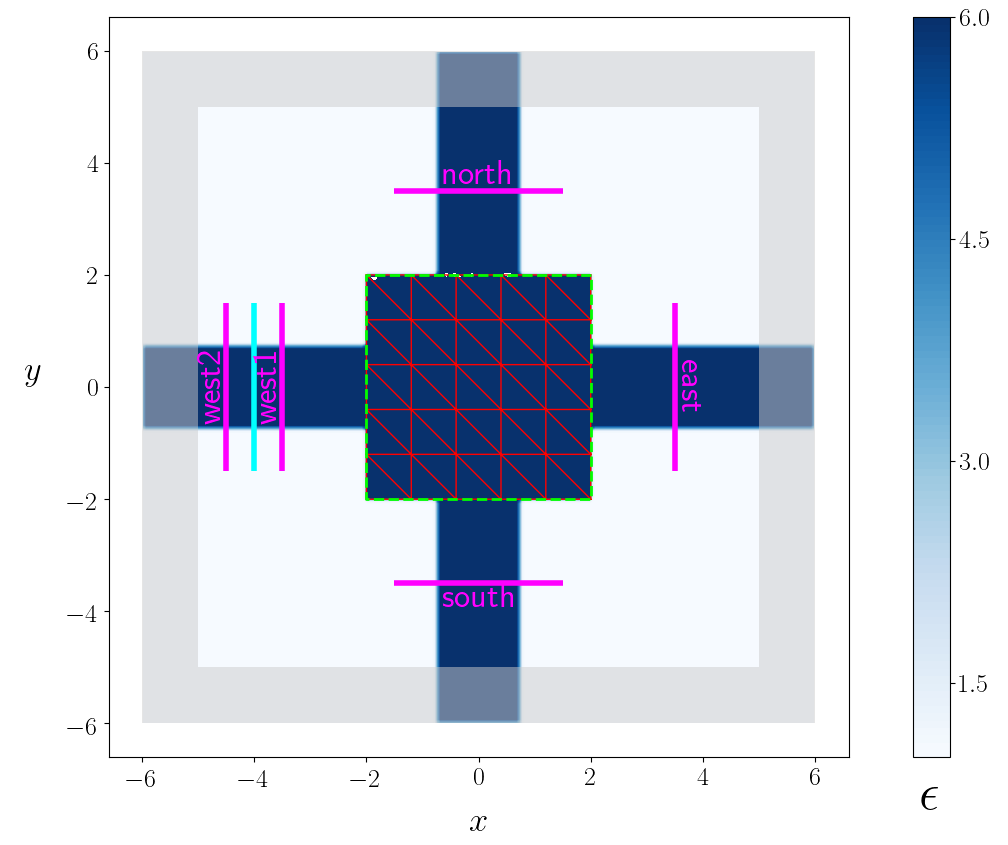
For the router problem, the design region is the square-shaped region outlined by the dashed green line in the figure above, and the fixed material geometry consists of just the four waveguide stubs emanating from it:

#----------------------------------------------------------------------
#- geometric objects (material bodies), not including the design object
#----------------------------------------------------------------------
wvg_mat    = mp.Medium(epsilon=eps_wvg)
east_wvg   = mp.Block(center=V3(ORIGIN+0.25*sx*XHAT), material=wvg_mat, size=V3(0.5*sx, w_east,  h) )
west_wvg   = mp.Block(center=V3(ORIGIN-0.25*sx*XHAT), material=wvg_mat, size=V3(0.5*sx, w_west,  h) )
north_wvg  = mp.Block(center=V3(ORIGIN+0.25*sy*YHAT), material=wvg_mat, size=V3(w_north, 0.5*sy, h) )
south_wvg  = mp.Block(center=V3(ORIGIN-0.25*sy*YHAT), material=wvg_mat, size=V3(w_south, 0.5*sy, h) )

background_geometry = [ east_wvg, west_wvg, north_wvg, south_wvg ]

We will pass this list as the background_geometry parameter to the OptimizationProblem constructor.

Background and foreground geometries

The label background_geometry for this list of objects refers to the fact that, in the full list of geometric_object structures that eventually gets passed to meep , they precede (lie beneath) the object describing the design region; thus, any portions of these objects that extend into the design region are covered by the design object and don’t show up in the computational geometry. For geometries in which portions of the fixed geometry lie logically above the design object, the optional constructor argument foreground_geometry may be used to specify a list of geometric_objects to come after the design-region object in the global list.

1C. Delineate functional subregions

Next we will delineate various subregions of the computational cell as being of particular significance. Again, this step will be familiar to anyone who has ever defined a FluxRegion (or FieldRegion or ForceRegion or EnergyRegion or ModeRegion or …) with the slight twist that the full panoply of distinct, specialized data structures for spatial regions in core meep (which includes the five just mentioned, plus some others) is replaced in meep_adjoint by the single new class Subregion.

Subregions in meep_adjoint

A subregion in meep_adjoint is simply a hyperrectangular region of space lying within the boundaries of the FDTD grid. A subregion may be of codimension 1 (i.e. a line in a 2D geometry or a plane in a 3D geometry), in which case it has a well-defined normal direction. Alternatively, subregions may be of codimension 0 [i.e. have the full dimensionality of the ambient space: a rectangle (2D) or box (3D)] or of dimension 0 (i.e. a set of discrete spatial points); in these cases the normal direction is undefined. Whereas the core meep solver treats each of these possibilities as distinct entities described by separate data structures—and further differentiates even among subregions of identical dimensionality based on the purpose for which the subregion is used in an FDTD calculation—meep_adjoint considers spatial regions of all (co-)dimensionalities and functional significance to be subcases of a common general entity, described by the single python class Subregion.

A further distinction is that each Subregion. in meep_adjoint has a name—a unique character-string identifier that may be chosen arbitrarily by users, or is assigned automatically if left unspecified. (The assignment of unique names to subregions is something that would probably be fairly useful even in core meep , but is essential in meep_adjoint to yield a natural, canonical naming convention for physical quantities like Poynting fluxes and energy densities)

Notwithstanding these differences, the instantiation of Subregions is syntactically almost identical to the instantiation of e.g. FluxRegion or FieldRegion structures in core meep scripts, as the examples below illustrate.

The initialization phase of a typical meep_adjoint problem involves defining three distinct functional categories of Subregion: source regions, objective regions, and the design region. The first two of these will be familiar to anyone who has ever created a Simulation , while the third is optimization-specific and has no analogue in core meep . (As an optional fourth category, you can also provide a list of “extra” subregions belonging to none of the above categories).

1. source_region: Location of excitation sources

When creating an OptimizationProblem for a simulation model in which the FDTD excitation source is relatively simple—namely, a single EigenmodeSource or constant-amplitude volume source confined to a single Subregion—it suffices to pass that Subregion as the source_region constructor parameter; then it will be used, together with package-wide configuration options like fcen and source_component or source_mode, internally within meep_adjoint to construct appropriate Source structures for forward FDTD simulations.

source_region is a convenience shortcut for sources

The use of source_region together with global configuration variables to define sources is actually a convenience option provided as a shortcut for simple source configurations.[#f3]_ The more general way to define forward sources for your problem is to instantiate a list of MeepSource structures and pass it as the sources parameter to the OptimizationProblem constructor, in which case you would not specify source_region.

2. objective_regions: Declaring sites at which we want frequency-domain fields and associated physical quantities

Next we specify all the subregions over which we will ask the FDTD solver to tabulate frequency-domain fields. This is another step that will be familiar to anybody who has ever written a core meep script, but again with slightly different (simpler!) mechanics. In a core meep script, for each subregion of interest we would execute a two-step procedure:

  1. We would first define the subregion of interest by creating a FluxRegion or FieldRegion or EnergyRegion (or other specialized subregion class) depending on the functional objective we have in mind.

  2. Then we would pass this object as a parameter to an API method like Simulation.add_flux or Simulation.add_energy to request computation of frequency-domain Poynting fluxes or energy densities for the given region.

meep_adjoint simplifies this by (a) collapsing all of the distinct data structures for physical subregions in step 1 to the single class Subregion, and (b) eliminating step 2. Thus, the only thing you need to do to declare your interest in frequency-domain fields in a given region of the computational cell is to create a Subregion and add it to the list passed as the objective_regions parameter to the OptimizationProblem constructor.

For the router problem, the frequency-domain quantities we want are just the fluxes into or out of each port, so we create codimension-1 Subregions for each of the waveguide stubs:

#----------------------------------------------------------------------
#- objective regions
#----------------------------------------------------------------------
n_center   = ORIGIN + d_flux*YHAT
s_center   = ORIGIN - d_flux*YHAT
e_center   = ORIGIN + d_flux*XHAT
w1_center  = ORIGIN - d_flux*XHAT
w2_center  = w1_center - (l_stub/3.0)*XHAT

north      = Subregion(center=n_center,  size=2.0*w_north*XHAT, dir=mp.Y,  name='north')
south      = Subregion(center=s_center,  size=2.0*w_south*XHAT, dir=mp.Y,  name='south')
east       = Subregion(center=e_center,  size=2.0*w_east*YHAT,  dir=mp.X,  name='east')
west1      = Subregion(center=w1_center, size=2.0*w_west*YHAT,  dir=mp.X,  name='west1')
west2      = Subregion(center=w2_center, size=2.0*w_west*YHAT,  dir=mp.X,  name='west2')

objective_regions = [north, south, east, west1, west2]
3. design_region: Informing `meep_adjoint` where it is allowed to vary the permittivity

As noted above, we don’t need to create any GeometricObjects for the tweakable region of the device geometry, but we do need to define the bounding box of this region via the Subregion-valued constructor parameter design_region. For the router geometry, the design region is a square of side length l_design centered at the origin:

#----------------------------------------------------------------------
#- design region
#----------------------------------------------------------------------
design_center = ORIGIN
design_size   = [l_design, l_design, h]
design_region = Subregion(name='design', center=design_center, size=design_size)

design_region is a convenience shortcut for basis

Just as source_region is a convenience shortcut for the more general sources, design_region is a convenience shortcut for the more general basis parameter to the OptimizationProblem constructor. If design_region is specified, it is used together with the meep_adjoint configuration options element_type and element_length to construct a FiniteElementBasis for the given region with elements of the given type and length. If you have a non-rectangular design region and/or non-finite-element basis set, just instantiate your own instance of Basis and pass it as the basis parameter to the OptimizationProblem constructor.

4. extra_regions: Additional subregions not covered by the above

In some cases you may want to specify additional subregions of the computational cell, not covered by any of the above categories, for which to request computation of frequency-domain fields. The optional extra_regions parameter may be used to pass a list of such regions. (API Note: This is technically superfluous, as extra subregions could just be tacked on to the objective_regions list, but maybe retaining extra_regions will make codes easier to read and understand?)

1D. Define the objective function

The last item to specify is the objective function that we are trying to maximize. This is just a character string, passed as the f_obj parameter to the OptimizationProblem constructor, defining a mathematical function in which one or more objective quantities appear as variables. 4 (As discussed here, objective quantities have canonical names like S_North or UE_Box formed by pairing a physical-quantity code–such as S for Poynting flux or UE for electric-field energy—with the name of a subregion as specified by the --name parameter to the Subregion constructor.)

For the right-angle router, our goal is simply to maximize power outflux through the North waveguide port, so we could take the objective function to be just the Poynting flux (objective quantity code: S) measured at the objective region we named North, i.e.:

fobj_router = 'S_North'

This is about as simple as an objective function can possibly get, and attempts at automated optimization with this objective do in fact produce somewhat improved designs. However, as it happens, there is an alternative way to define an objective function for this problem that yields significantly better final outcomes: instead of optimizing for maximal power outflux, we optimize for maximal overlap with the forward-traveling eigenmode of the North waveguide, taking the objective function to be the squared modulus of the eigenmode expansion coefficient for forward-traveling mode 1 (objective quantity code: P1 or F1):

fobj_router = '|P1_North|^2'

So these are the objective functions to choose if we want our optimized design to be a right-angle router. On the other hand, if instead we want a three-way symmetric splitter with maximal equality of output power from north, south, and east, then we need an objective function that penalizes discrepancies in outgoing flux—something like:

fobj_splitter = '-( S_north - S_east )^2  -( S_east - S_south )^2 - (S_south - S_north)^2

or:

fobj_splitter = '-( |P1_north| - |P1_east| )^2  -( |P1_east| - |M1_south| )^2 -(|M1_south| - |P1_north|)^2'

In router.py we select one or another of these objective functions depending on command-line arguments:

objective_function = fobj_splitter if args.splitter else fobj_router

1E. Instantiate the OptimizationProblem

The final step is to invoke the OptimizationProblem constructor with the various parameter values initialized above. In router.py this is done at the end of the init_problem routine, which returns the new class instance:

return OptimizationProblem(
 cell_size=cell_size,
 background_geometry=background_geometry,
 source_region=source_region,
 objective_regions=objective_regions,
 design_region=design_region,
 extra_regions=[full_region]
 objective_problem=objective,
 extra_quantities=extra_quantities
)

Phase 2: Interactive exploration

As discussed above, the goals of the interactive phase are

  • to sanity-check our work in the previous phase by investigating the OptimizationProblem we constructed and confirming that it correctly describes the design problem we want to solve, and

  • to get a sense of the computational cost of evaluating the objective function and the practical feasibility of achieving our desired performance targets, which will help us in the following phase to make reasonable choices for various parameters controlling the automated design iteration.

We begin the interactive phase by invoking the init_problem routine in the router.py script, which executes the initialization procedure detailed above and returns a new instance of OptimizationProblem:

>>> import router
>>> prob = router.init_problem()

Now our python session contains a new OptimizationProblem named prob.

2A. Visualizing the geometry

The most basic sanity check is to inspect a graphical visualization of the problem geometry to make sure the problem we specified is the one we wanted. For this purpose, the meep_adjoint package contains a built-in visualization module that reduces the task of visualizing a geometry to a one-liner:

>>> prob.visualize()

This should produce an image like the following:

../_images/RouterGeometry0.png

This

Customizing the visualization

prob.visualize()

2B. Updating the design function

prob.update_design(design='2 + cos(3*x)*sin(2*y)')
prob.visualize()

2C. Compute objective function value and gradient

fq, _ = prob(need_gradient = False)

_ , gradf = prob(need_value = False)

2D. Displace design variables in direction of gradient and check that objective function improves

Phase 3: Automated optimization

1

To clarify, these are the sources for the forward simulation; sources for the adjoint simulation are determined automatically within meep_adjoint.

2

More specifically, the following configuration options are referenced: fcen, df, source_mode, and source_component.

If source_mode>=1, the source is an EigenmodeSource for the eigenmode of the given index; in this case the source_component option is not referenced.

Otherwise (i.e. source_mode==0), the source is an ordinary Source with component determined by the value of source_component (which should be a string like Ex or Hy).

3

Specifically, eigenmode sources—or volume sources with spatially uniform amplitude—lying within a single SubRegion and having Gaussian temporal envelope.

4

It is perfectly legal to define objective functions that don’t depend on any objective quantities, but then the objective-function value would be independent of the design variables and the optimization problem would be trivial.