Skip to content

Diffraction patterns for discs, disc arrays, and hole arrays in metal screens

In this example, we shine a laser beam (or a plane wave) on an (infinite-area) metal screen perforated by a square-lattice array of circular holes, and produce images of the diffraction patterns as observed on a visualization surface located behind the perforated screen. Here's a schematic depiction of the configuration:

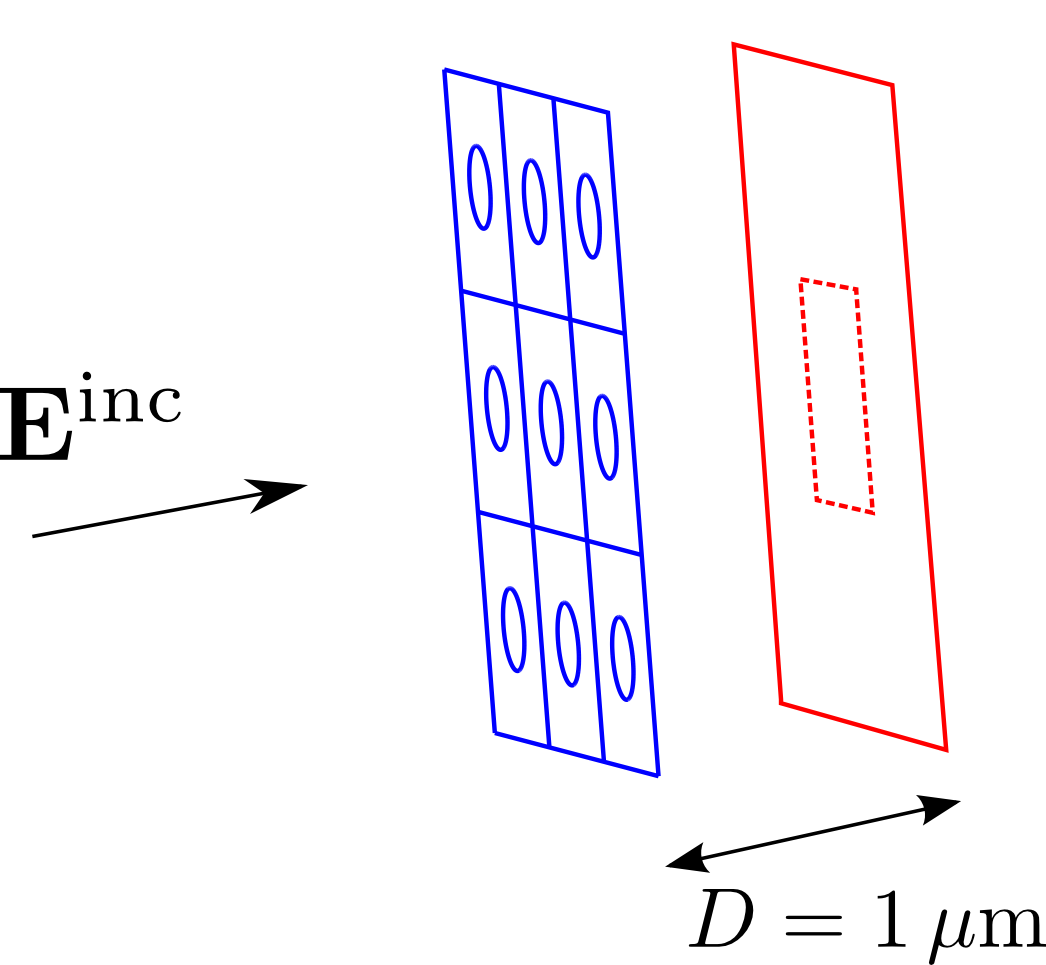
Diffraction experiment image

The files for this example may be found in the share/scuff-em/examples/DiffractionPatterns subdirectory of your scuff-em installation.

gmsh geometry file and surface mesh for the screen unit cell

The gmsh geometry file HoleyScreenUnitCell.geo describes an (infinitely thin) square metallic screen, of dimensions 1μm × 1μm, with a hole of radius 0.25 μm centered at the center of the square. I produce coarser and finer surface meshes for this geometry by saying

% gmsh -2 -clscale 1 HoleyScreenUnitCell.geo
% RenameMesh HoleyScreenUnitCell.msh
% gmsh -2 -clscale 0.75 HoleyScreenUnitCell.geo
% RenameMesh HoleyScreenUnitCell.msh

(where RenameMesh is a simple bash script that uses scuff-analyze to count the number of interior edges in a surface mesh and rename the mesh file accordingly.) This produces the files HoleyScrenUnitCell_1228.msh and HoleyScreenUnitCell_2318.msh, which you can visualize by opening in gmsh:

% gmsh HoleyScreenUnitCell_1228.msh
% gmsh HoleyScreenUnitCell_2318.msh

Coarse Holey screen mesh image

Fine Holey screen mesh image

Note that finer meshing resolution is obtained by specifying the -clscale argument to gmsh (it stands for "characteristic length scale"), which specifies an overall scaling factor for all triangle edges.

scuff-em geometry files

The scuff-em geometry files HoleyScreen_1228.scuffgeo and HoleyScreen_2318.scuffgeo describe infinite square lattices with unit cells defined by the unit-cell meshes we created above. The N=1228 guy looks like this:

LATTICE
        VECTOR 1 0
        VECTOR 0 1
ENDLATTICE    

OBJECT HoleyScreen
        MESHFILE HoleyScreenUnitCell_1228.msh
ENDOBJECT

Note that we don't have to specify a MATERIAL for the screen, since PEC is the default.

We can use scuff-analyze to produce an image of what the full geometry looks like, including the lattice repetitions:

% scuff-analyze --geometry HoleyScreen_1228.scuffgeo --WriteGMSHFiles --Neighbors 2

This produces the file HoleyScreen_1228.pp, which you can view by opening it in gmsh:

% gmsh HoleyScreen_1228.pp

HoleyScreen geometry image

Field visualization mesh

The next step is to create a meshed representation of the surface on which we will visualize the diffraction patterns. Here's a gmsh file called FVMesh.geo that describes a square of side length 1 micron, parallel to the xy plane and located at a height of z=1 micron, thus corresponding to the region enclosed by the dotted line in the schematic figure above. ("FVMesh" stands for "field-visualization mesh.") This .geo file contains a user-specifiable parameter N that sets the number of triangle edges per unit length in the mesh representation; I would like to set this number to 50, so I say

% gmsh -2 -setnumber N 50 FVMesh.geo -o FVMesh.msh
% RenameMesh FVMesh.msh

This produces the file FVMesh_7400.msh:

FVMesh image

Running scuff-scatter

Now all that's left is to run the calculation. Put the following content into a little text file called scuff-scatter.args and pipe it into the standard input of scuff-scatter:

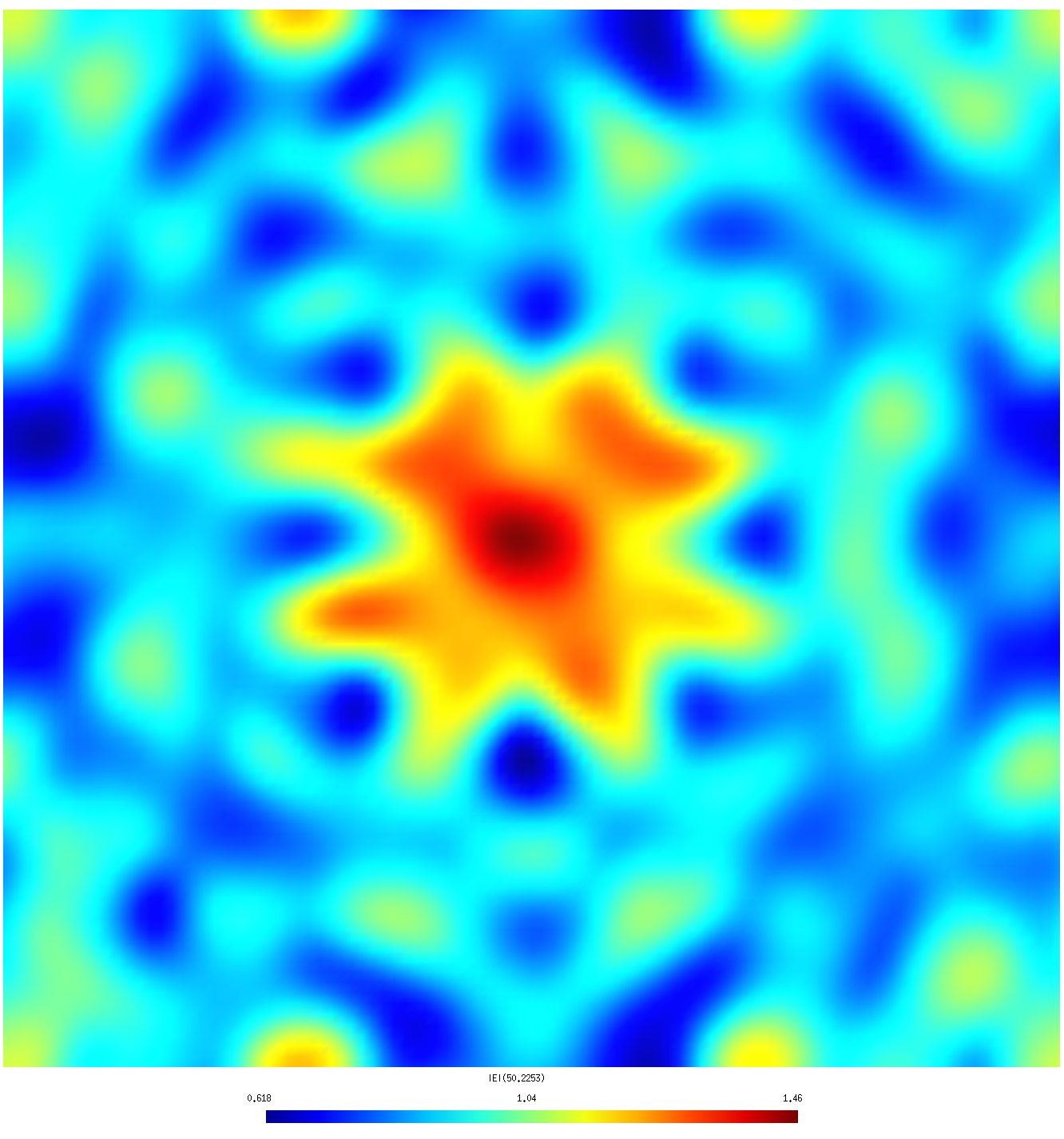
geometry        HoleyScreen_1228.scuffgeo
FVMesh          FVMesh_7400.msh
Lambda          0.3751
Lambda          0.2501
Lambda          0.1251
pwDirection     0 0 1
pwPolarization  1 0 0

Note that I have chosen wavelengths of where m is the hole radius. In each case I have shifted the wavelength by a tiny amount away from being commensurate with the lattice period to avoid numerical instabilities associated with Wood anomalies.

 % scuff-scatter < scuff-scatter.args
 % scuff-scatter --geometry HoleyScreen_2318.scuffgeo < scuff-scatter.args

In the second command line here, the command-line specified geometry overrides the geometry in the .args file.

This produces the files HoleyScreen_1228.FVMesh_7400.pp and HoleyScreen_2318.FVMesh_7400.pp, which can be visualized by opening them in gmsh.

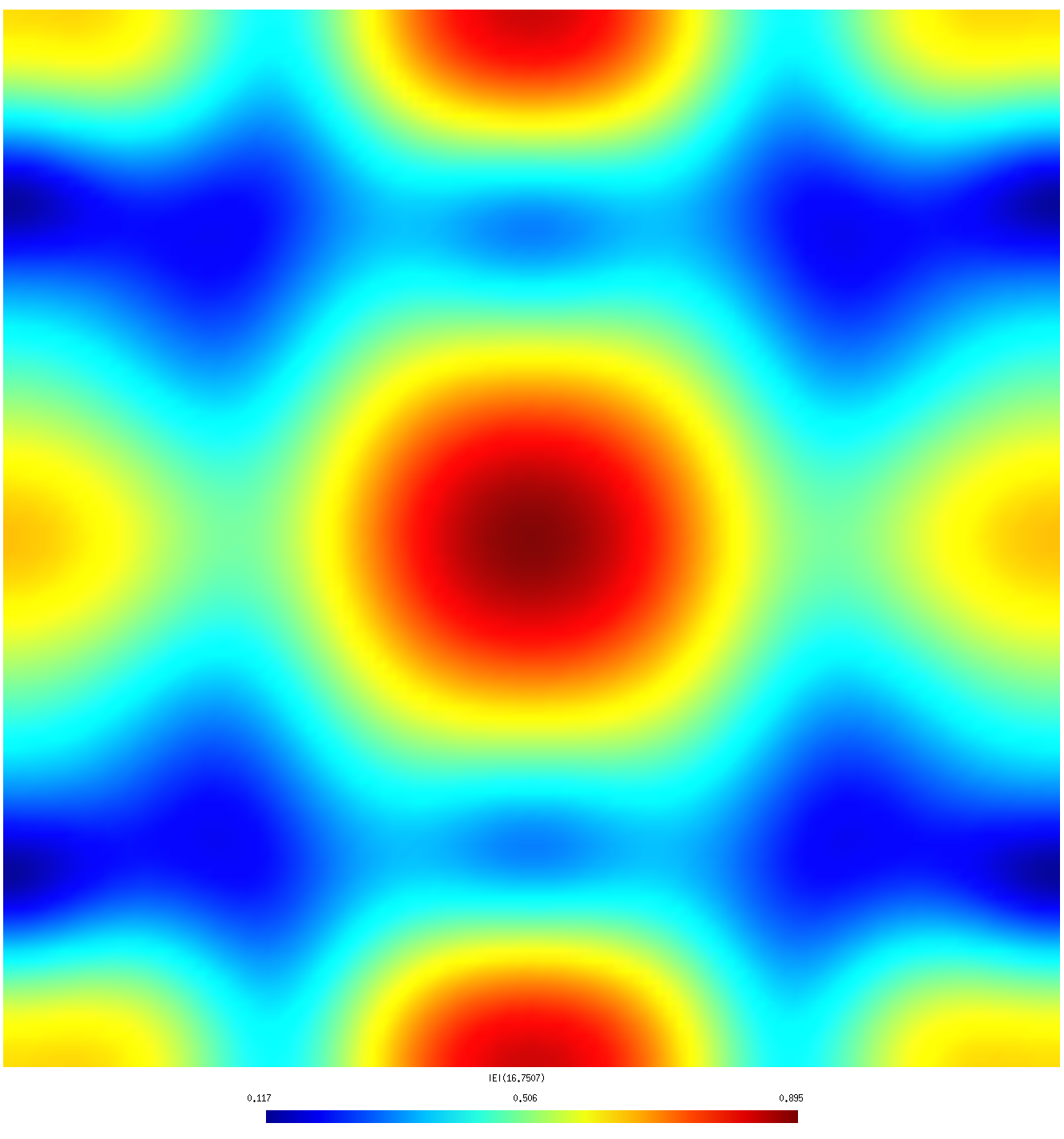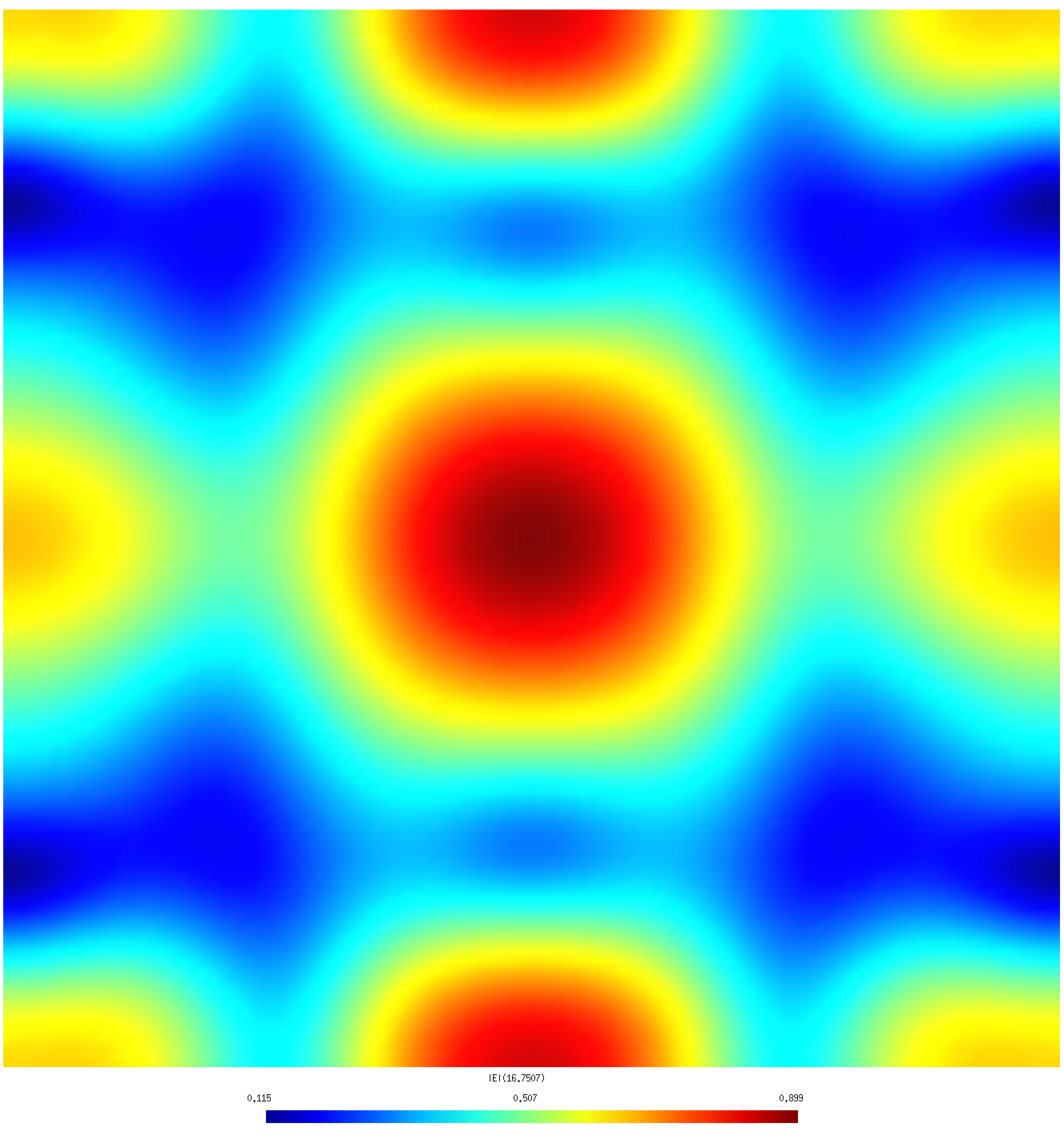λ=1.5 R (coarse mesh) λ=1.5 R (fine mesh)
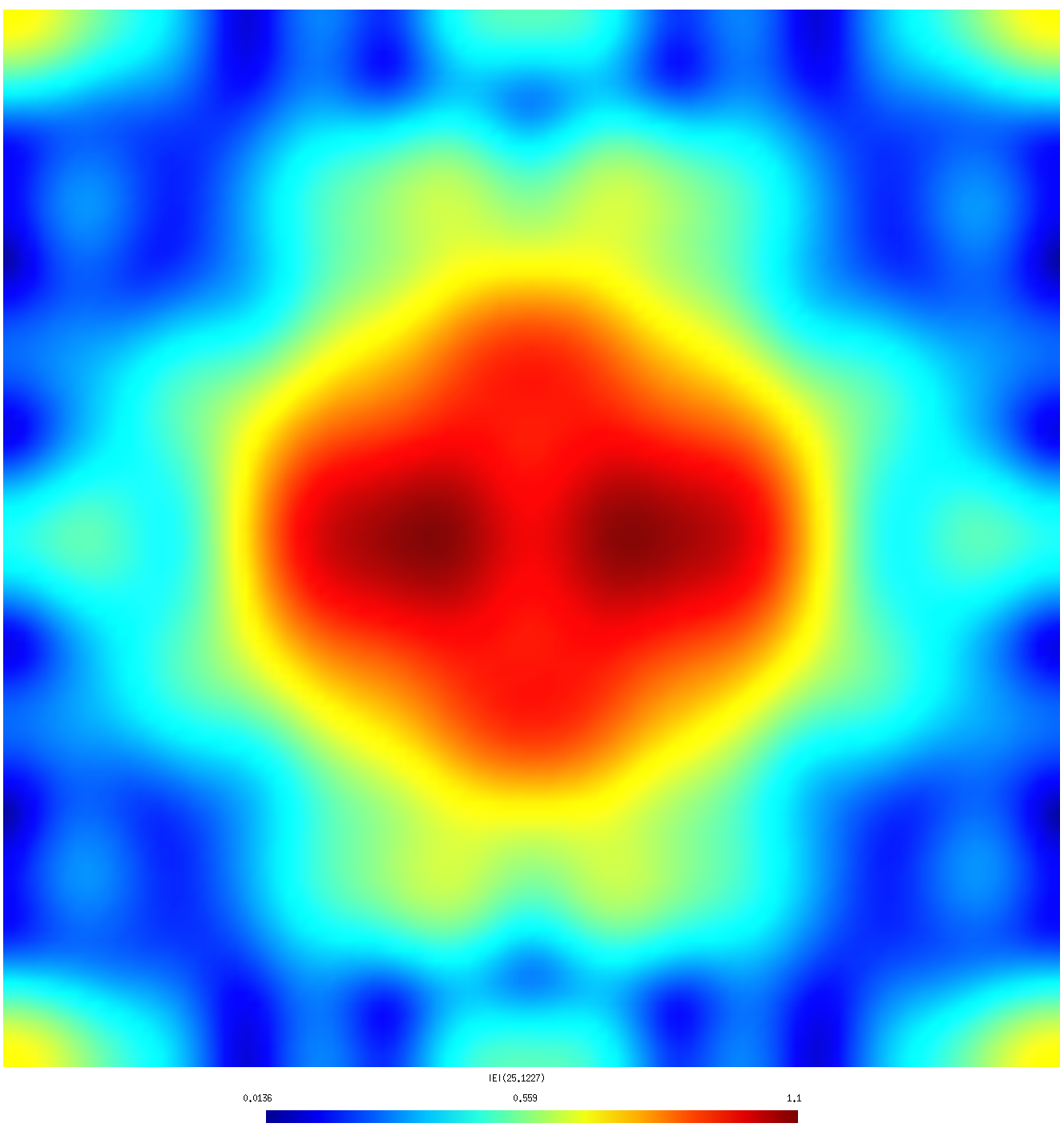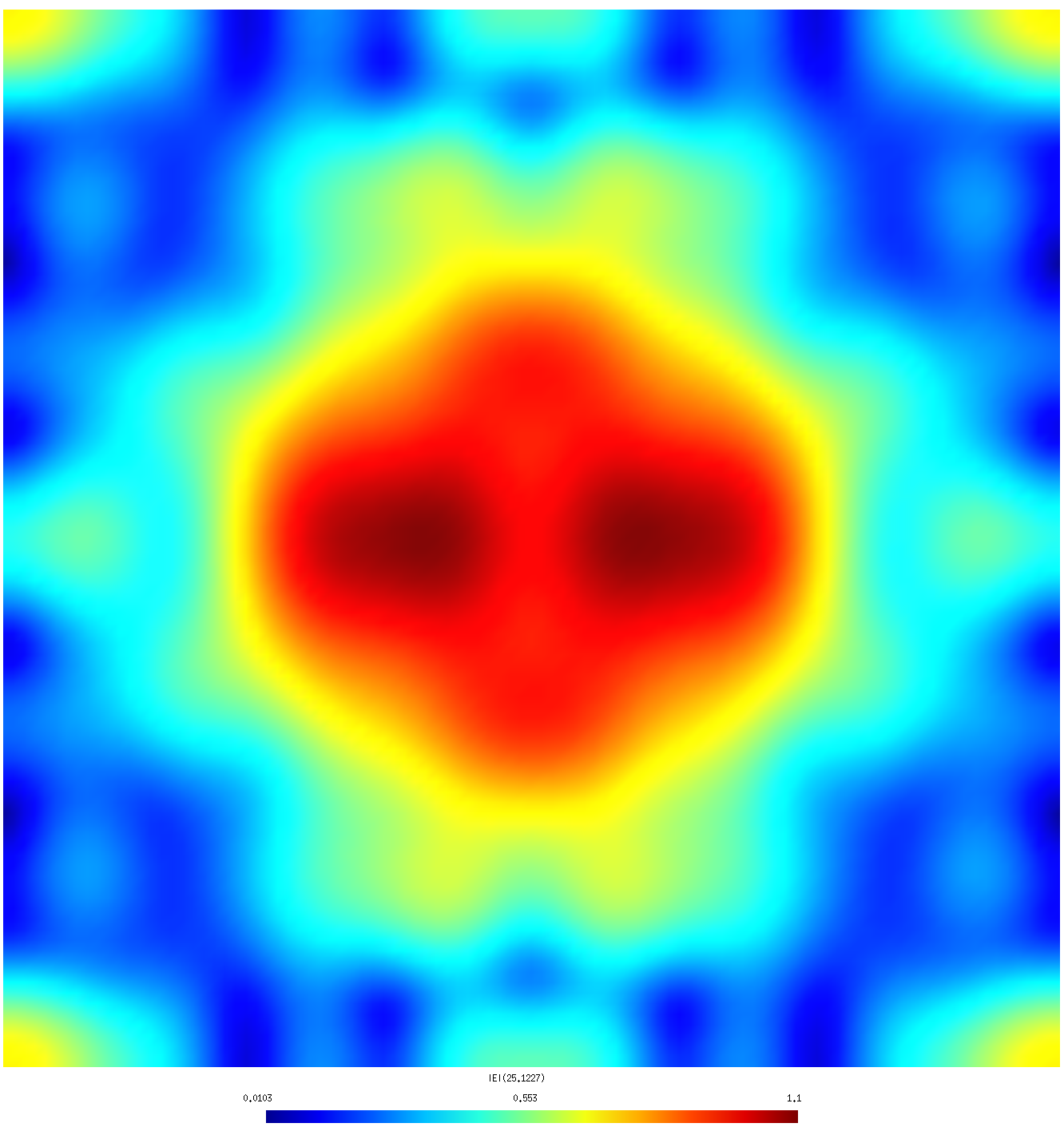λ=1.0 R (coarse mesh) λ=1.0 R (fine mesh)
λ=0.5 R (coarse mesh) λ=0.5 R (fine mesh)

Comments