

Brillouin-zone integration in scuff-em

Many codes in the scuff-em suite require evaluating integrals over the Brillouin zone (BZ) of a 1D or 2D reciprocal lattice, i.e.

$$Q(\omega) = \int_\text{BZ} \overline{Q}(\omega, \mathbf{k}_\text{B}) \,d\mathbf{k}_\text{B}$$

where we generically use the overlined symbol $\overline{Q}(\mathbf{k}_\text{B})$ to denote the contribution of Bloch vector $\mathbf{k}_\text{B}$ to quantity $Q$. Examples of calculations that require Brillouin-zone integrations include

• the Casimir force per unit imaginary frequency $\omega=i\xi$ on an extended object in scuff-cas3d

• the Casimir-Polder potential per unit imaginary frequency $\omega=i\xi$ experienced by a polarizable particle near an extended surface in scuff-caspol

• the local density of states at a given angular frequency $\omega$ at user-specified evaluation points in scuff-ldos.

In general, Brillouin-zone integrations are evaluated by numerical cubature---that is, as weighted sums of integrand samples: $$Q(\omega) \approx \sum w_n \overline Q(\omega, \mathbf{k}_n)$$ where $\{w_n, \mathbf{k}_n\}$ are the weights and points in a cubature rule for the Brillouin zone of your reciprocal lattice, and where each integrand sample $\overline Q(\omega, \bf k_n)$ is computed by performing a single scuff-em calculation at a fixed Bloch wavevector. The scuff-em workflow offers two options for evaluating such cubatures:

• You can design and implement your own cubature scheme involving your own custom-chosen weights and points $\{w_n, \bf k_n\}$. In this case, you will use the --byOmegakBloch command-line option to instruct a scuff-em application code to report values of the quantity $\overline Q(\omega, \bf k_n)$ at each of your points (this output will typically be written to file with extension .byOmegakBloch or .byXikBloch), then compute the weighted sums yourself in e.g. julia.

 

• Alternatively, you can ask scuff-em to perform the BZ integration internally, using one of several built-in cubature schemes. In this case the BZ-integrated quantities $Q(\omega)$ will typically be written to an output file with extension .byOmega or .byXi. You will also get an output file named .byOmegakBloch or .byXikBloch that reports the Bloch-vector-resolved integrand samples $\overline Q(\omega, \bf k_n)$ chosen internally by the scuff-em BZ integrator.

Command-line options for customizing internal BZ integration

If you choose the second option above, you may specify various command-line options to customize the algorithm used by scuff-em to select the cubature points and weights $\{w_n, \mathbf{k}_n\}$. The options are listed here and discussed in more detail below.

--BZIMethod [CC | TC | Polar | Polar2]

Selects the integration algorithm (see below for details).

--BZIOrder NN

Sets the order (accuracy parameter) of the integration algorithm to NN. The allowed values of NN here depend on the integration algorithm you chose (see below).

--BZIRelTol xx
--BZIAbsTol xx
--BZIMaxEvals NN

For adaptive integration algorithms in which the order is determined internally (see below), these options allow you to specify relative and absolute error tolerances and an upper limit on the number of integrand samples that will be used.

--BZSymmetryFactor [2|4|8]

This option lets you tell scuff-em that your integrand function $\overline Q(\mathbf k_\text{B})$ is invariant under 2, 4, or 8-fold rotational symmetry transformations applied to $\mathbf k_\text{B}$. See below for more details on what this means.

Understanding the internal BZ integration algorithms

To help you understand how to configure the various command-line options above, this section describes the various integration algorithms available and how they are affected by the command-line parameters.

Integration methods for 1D Brillouin zones

For one-dimensional Brillouin zones, there is only one BZ integration method available---namely, Clenshaw-Curtis quadrature (--BZIMethod CC, the default) with the number of integrand samples either fixed or chosen adaptively until user-specified error tolerances are achieved.

More specifically, you may say either

• --BZIOrder [11 | 13 | 15 | ... | 97 | 99]

or

• --BZIOrder 0

The former option selects fixed-order CC cubature with 11, 13, ... 99 sample points. (This number must be an odd integer between 11 and 99 inclusive.)

The latter option selects adaptive CC cubature using this algorithm. In this case the number of sample points will be chosen automatically subject to the values you select for the --BZIRelTol, --BZIAbsTol, and --BZIMaxEvals command-line options.

Symmetry factors for 1D Brillouin zones

For 1D Brillouin zones, the only allowed value of the --BZSymmetryFactor option is 2, indicating that your integrand is symmetric under sign flip of the Bloch wavevector, i.e. $\overline Q(k_x) = \overline Q(-k_x)$. In this case the BZ integration may be restricted to the range $0\le k_x \le \frac{\pi}{L_x}.$

Integration methods for 2D Brillouin zones

The following integration methods are implemented for 2D Brillouin zones. (See below for pictures of where the various methods place their sample points.)

• Clenshaw-Curtis cubature (--BZIMethod CC)

  Nested 2D fixed-order or adaptive Clenshaw-Curtis cubature.

  For fixed-order nested CC cubature with NN sample points per dimension, say --BZIOrder NN. Here NN must be an odd integer between 11 and 99 inclusive.

  For adaptive 2D CC cubature (subject to your specified values of --BZIRelTol, --BZIAbsTol, and --BZIMaxEvals) say --BZIOrder 0.

 

• Triangle cubature (--BZIMethod TC)

  This algorithm divides the Brillouin zone into 8 triangles and applies a fixed-order triangle cubature scheme to each triangle, omitting repetition of triangles that are symmetry-equivalent given the value you specified for --BZSymmetryFactor (see pictures below).

  For this algorithm, the allowed values of --BZIOrder are 1, 2, 4, 5, 7, 9, 13, 14, 16, 20, or 25.

 

• Polar cubature (--BZIMethod Polar)

  This algorithm uses a polar decomposition $(k_x,k_y) \to (k_\rho, k_\theta)$ to evaluate the BZ integral as two nested 1D integrals, one over $k_\rho$ and the second over $k_\theta$. (The $k_\rho$ integral is evaluated via Clenshaw-Curtis quadrature, and the $k_\theta$ quadrature is evaluated using rectangular-rule quadrature, not necessarily of the same order).

  This algorithm is useful for integrands that are strongly peaked near the origin of the Brillouin zone and highly attenuated near the boundaries, so that most of the integral comes from the region near the origin.

  For this algorithm, the number of integration points used for the $k_\rho$ and $k_\theta$ integrals (call these numbers $N_\rho$ and $N_\theta$) are encoded into the value passed to --BZIOrder in the form $100\times N_\rho + N_\theta,$ where $N_\rho$ and $N_\theta$ are each odd integers between 11 and 99 inclusive.

  Thus, for example, --BZIOrder 3321 specifies that the $k_\rho$ integral is to be evaluated via 33-point CC cubature, while the $k_\theta$ integral is to be evaluated via 21-point rectangular-rule cubature.

 

• Polar cubature with change of variables $k_\rho \to k_z$ (--BZIMethod Polar2)

  This is the same as --BZIMethod Polar, but with two modifications: (a) The $k_\rho$ integral is split into two separate integrals covering the ranges $k_\rho < k_0$ and $k_\rho >k_0$ (where $k_0\equiv \frac{\omega}{c}$ is the vacuum photon wavenumber at the frequency in question). (b) In each of the two $k_\rho$ integrals we make the change of variables $$k_\rho \to k_z\equiv \sqrt{|k_0^2 - k_\rho^2|}.$$

  These modifications are useful for cases in which the free-space wavevector $k_0$ falls within the Brillouin zone. In these cases, the convergence of the $k_\rho$ integral is degraded by the phenomena known as "Wood anomalies" in optics or "van Hove singularities" in solid-state physics, and changing variables to $k_z$ introduces a Jacobian factor that neutralizes these singularities to yield a better-behaved integrand.

Special $N_\theta$ values for rotationally-invariant integrands

As discussed above, for the Polar and Polar2 integration methods the value of the --BZIOrder option is interpreted as the composite quantity $100\times N_\rho + N_\theta$, where $N_\rho$ and $N_\theta$ are odd integers in the range $[11,99]$ specifying the number of cubature points used for the $k_\rho$ and $k_\theta$ integrals (or set to 0 to request adaptive quadrature).

For fully rotationally-symmetric geometries in which the BZ integrand $\overline{Q}$ is independent of $k_\theta$, you can specify $N_\theta=\{2,4,6\}$ to indicate that the $k_\theta$ integral is to be evaluated by a 1-point cubature with the single $k_\theta$ sample taken at $k_\theta=\{0,\frac{\pi}{2},\frac{\pi}{4}\}$.

(Of course, no geometry discretized into triangles can actually be fully rotationally invariant, but pretending so may be a reasonable approximation in some cases, such as this one.)

Symmetry factors for 2D Brillouin zones

For 2D geometries, the option --BZSymmetryFactor may take the value 2, 4, or 8, specifying that the Brillouin-zone integrand $\overline{Q}(k_x, k_y)$ obeys symmetries as follows:

• --BZSymmetryFactor 2:

  We have $\overline{Q}(k_x,k_y) = \overline{Q}(k_x,-k_y),$ so the BZ integration may be restricted to just the right half of the BZ.

 

• --BZSymmetryFactor 4:

  We have $\overline{Q}(k_x,k_y) = \overline{Q}(\pm k_x, \pm k_y),$ so the BZ integration may be restricted to just the upper-right quadrant of the BZ.

 

• --BZSymmetryFactor 8: In addition to symmetry under sign changes, the integrand is symmetric under $k_x\leftrightarrow k_y$, so the BZ integration may be restricted to the triangular region $0\le k_y \le k_x \le \frac{\pi}{L_x}.$ (This is only possible for square lattices.)

Locations of quadrature points for 2D Brillouin zones

Here are some diagrams indicating the Bloch wavevectors that will be sampled by the internal algorithms for Brillouin-zone integration with various values of the command-line parameters:

--BZIMethod CC    --BZIOrder  21    --BZSymmetryFactor 1

 

--BZIMethod CC    --BZIOrder  21    --BZSymmetryFactor 2

 

--BZIMethod CC    --BZIOrder  21    --BZSymmetryFactor 4

 

--BZIMethod CC    --BZIOrder  21    --BZSymmetryFactor 8

 

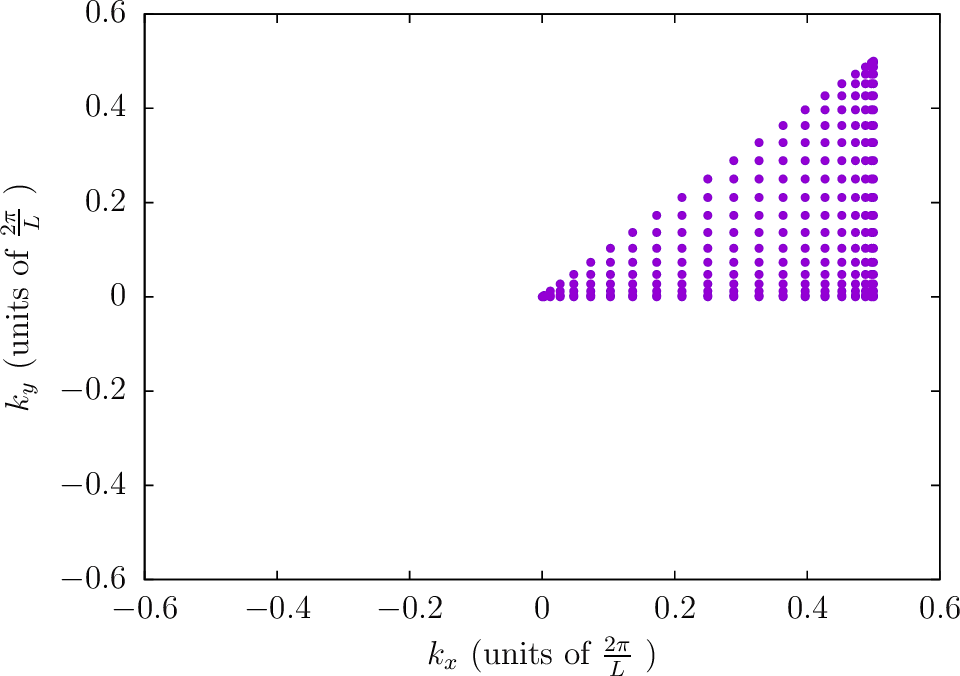
--BZIMethod TC    --BZIOrder  20    --BZSymmetryFactor 1

 

--BZIMethod TC    --BZIOrder  20    --BZSymmetryFactor 2

 

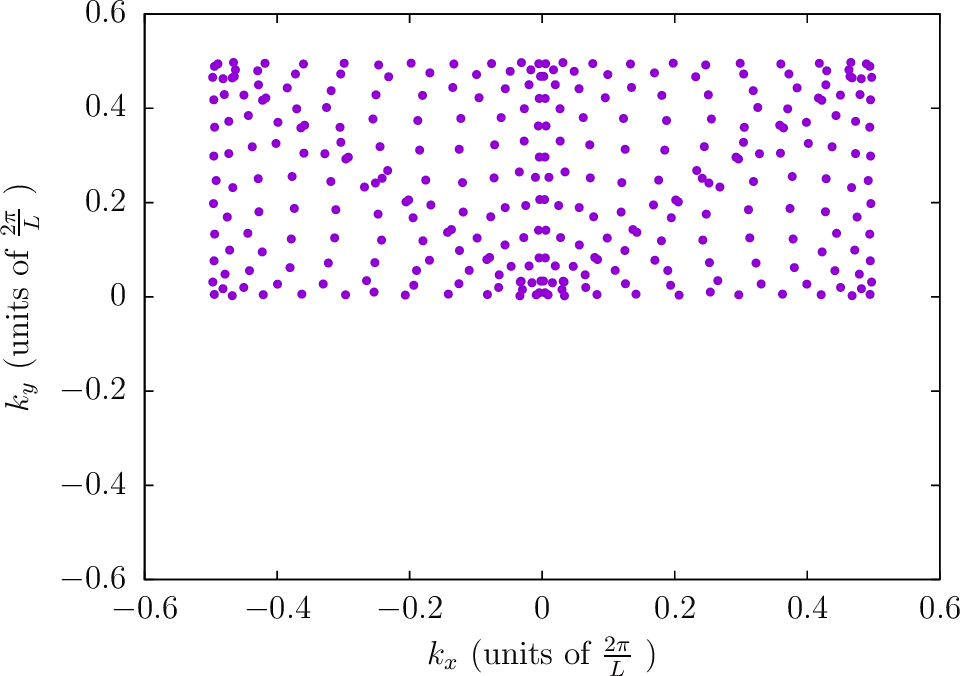
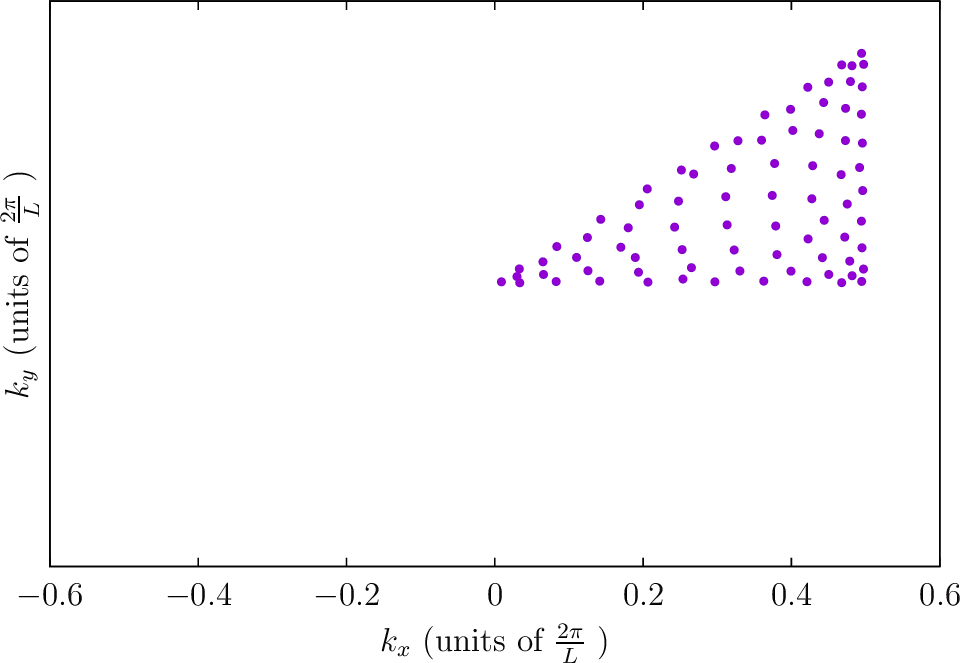
--BZIMethod TC    --BZIOrder  20    --BZSymmetryFactor 4

 

--BZIMethod TC    --BZIOrder  20    --BZSymmetryFactor 8

 

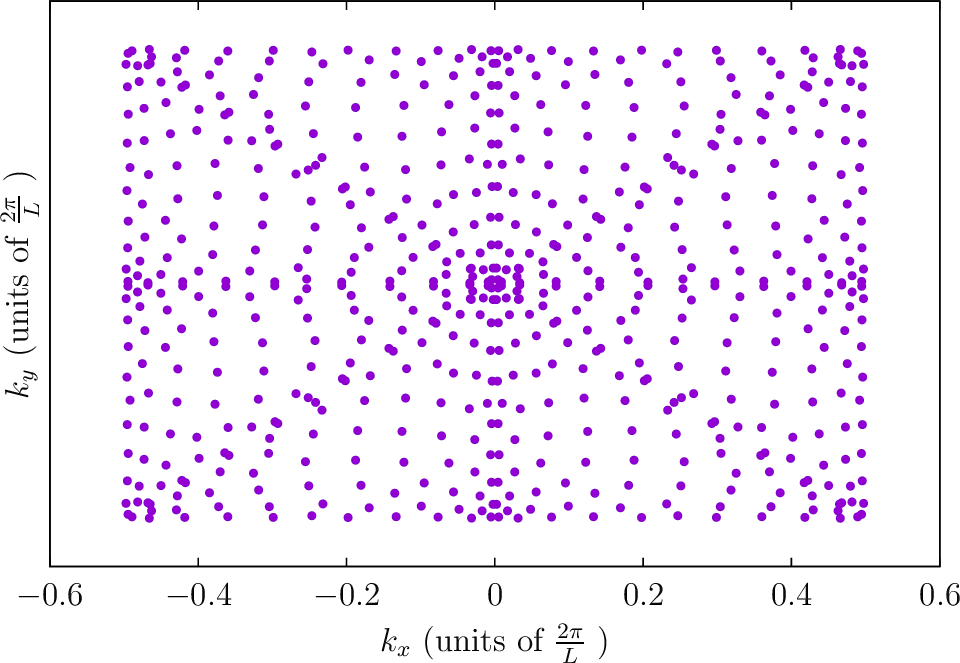
--BZIMethod Polar --BZIOrder 3111 --BZSymmetryFactor 1

 

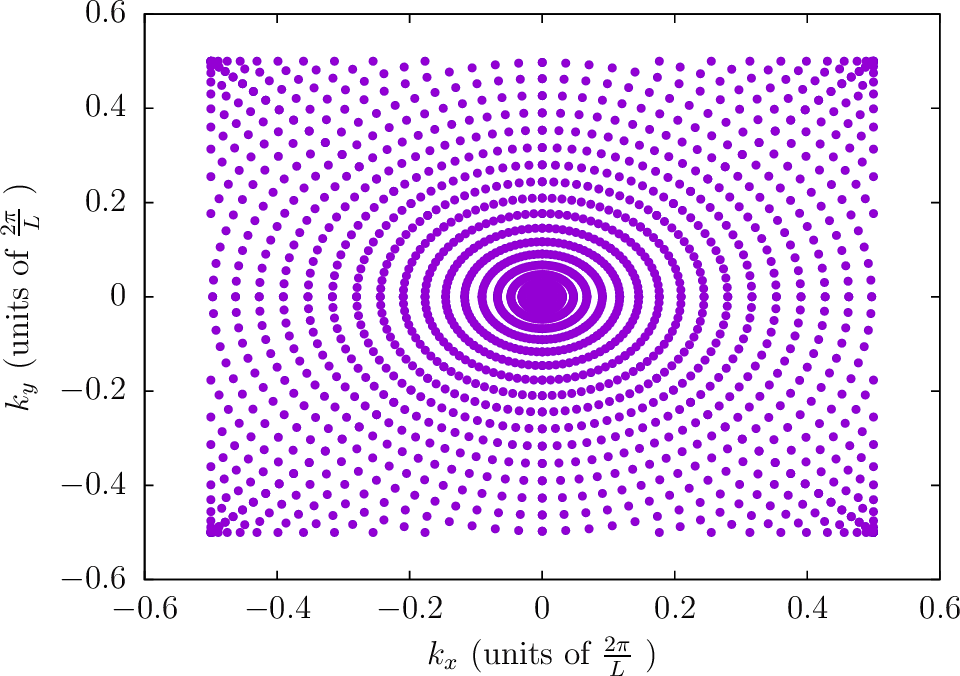
--BZIMethod Polar --BZIOrder 3111 --BZSymmetryFactor 2

 

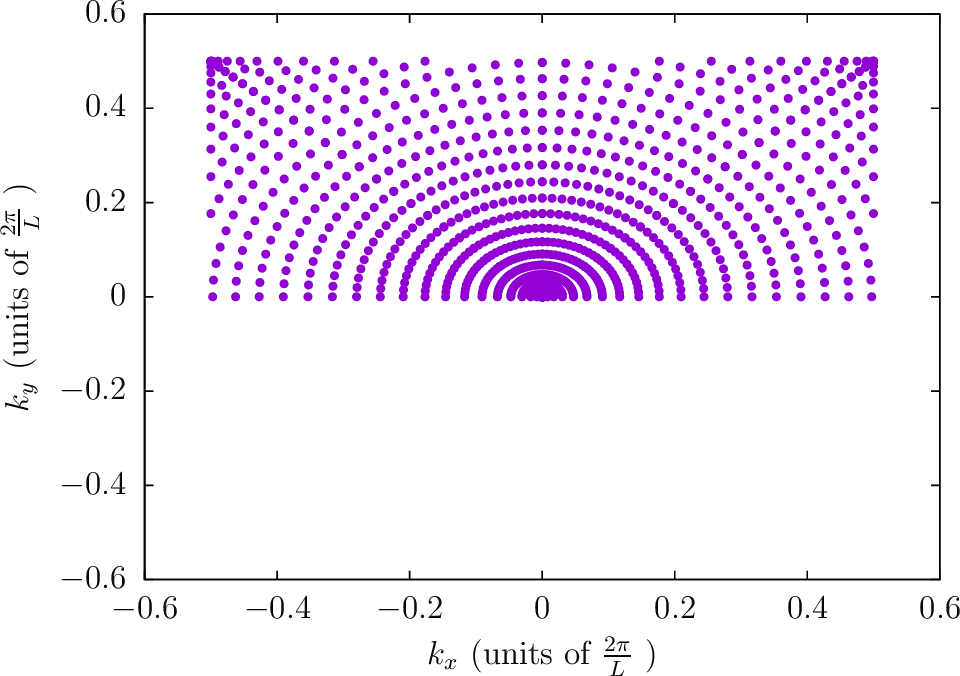
--BZIMethod Polar --BZIOrder 3111 --BZSymmetryFactor 4

 

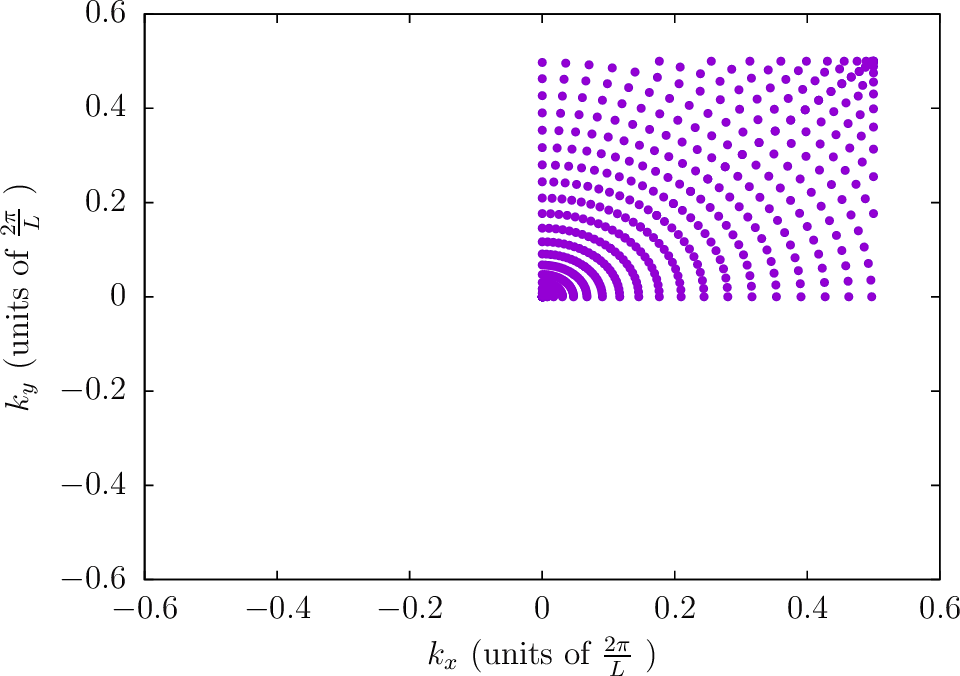
--BZIMethod Polar --BZIOrder 3111 --BZSymmetryFactor 8

 

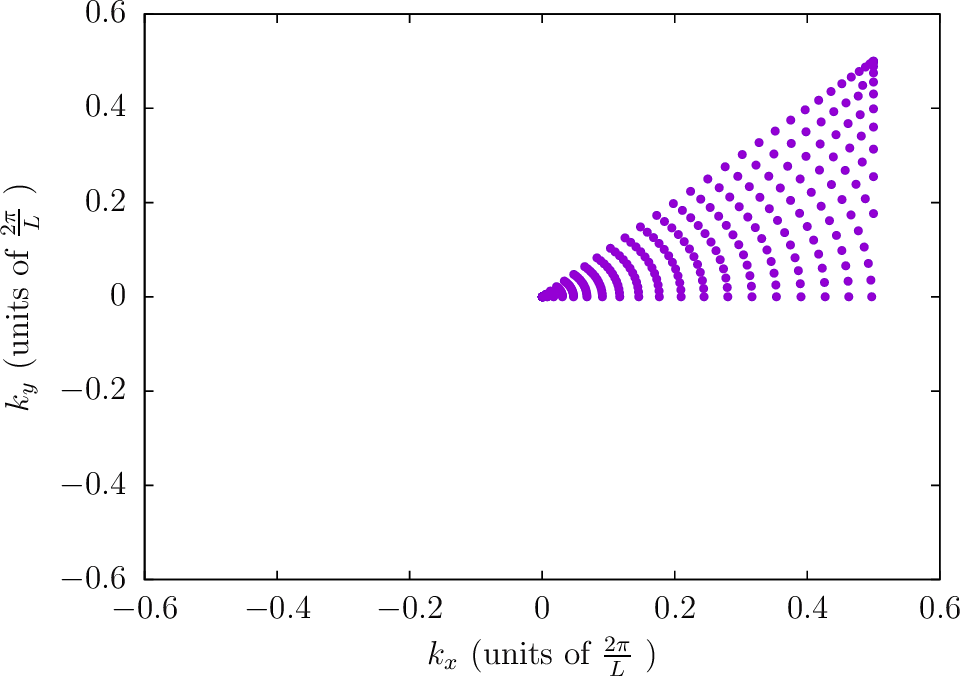
Note: The next four diagrams are for a frequency of $\frac{\omega}{c}\approx 0.32\cdot \frac{2\pi}{L}$. The accumulation of points near $|\mathbf{k}_\text{B}|=\frac{\omega}{c}$ is noticeable for the Polar2 integration strategy.

--BZIMethod Polar2 --BZIOrder 1111 --BZSymmetryFactor 1

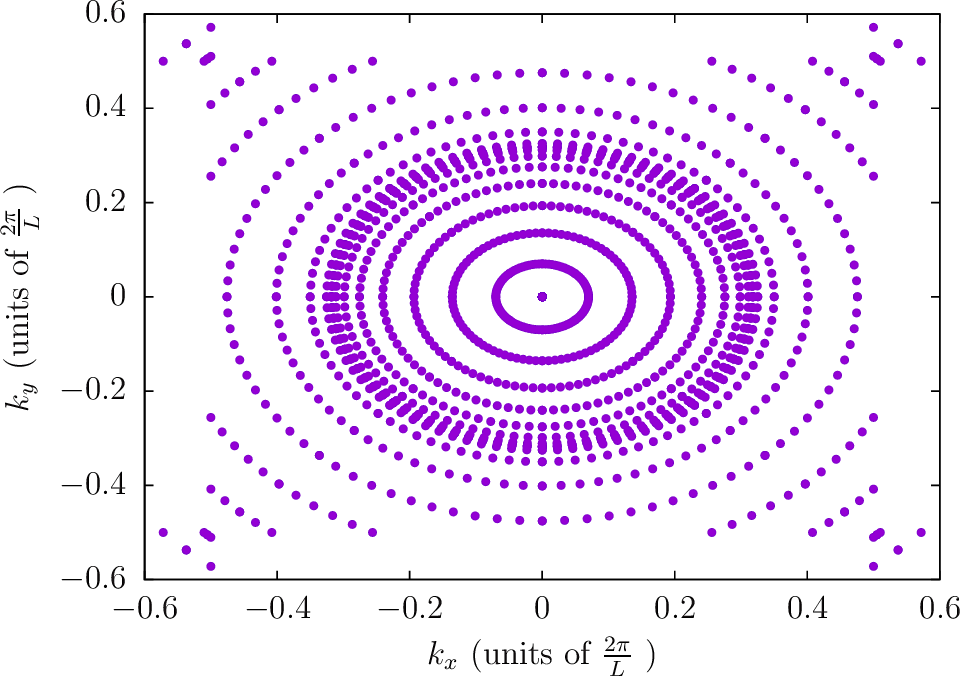
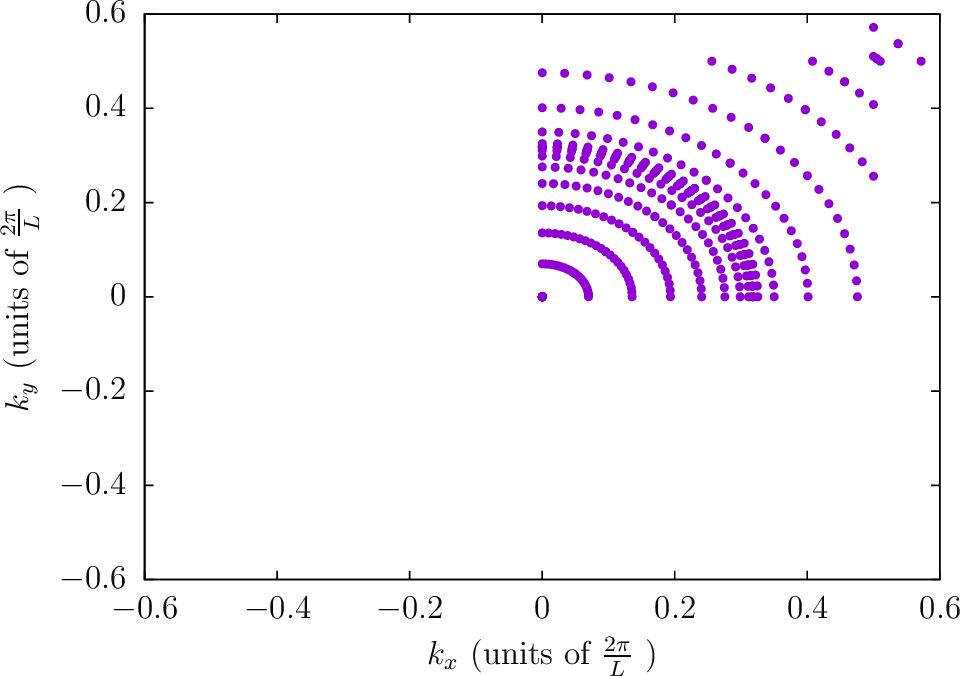
--BZIMethod Polar2 --BZIOrder 1111 --BZSymmetryFactor 2

--BZIMethod Polar2 --BZIOrder 1111 --BZSymmetryFactor 4

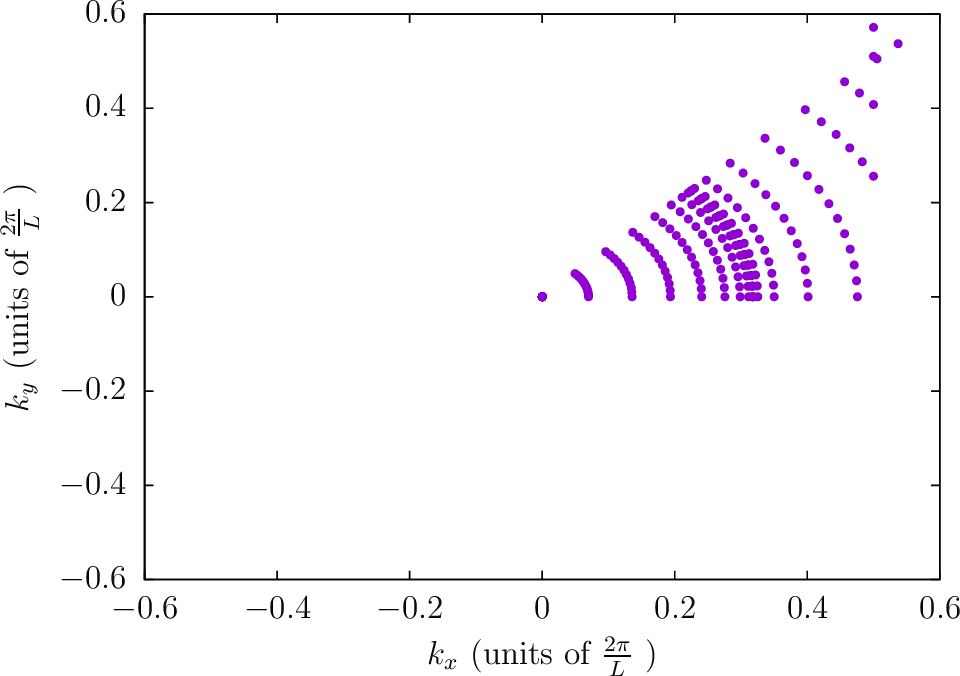
--BZIMethod Polar2 --BZIOrder 1111 --BZSymmetryFactor 8

Locations of quadrature points for 1D Brillouin zones

--BZIMethod CC    --BZIOrder  31    --BZSymmetryFactor 1

 

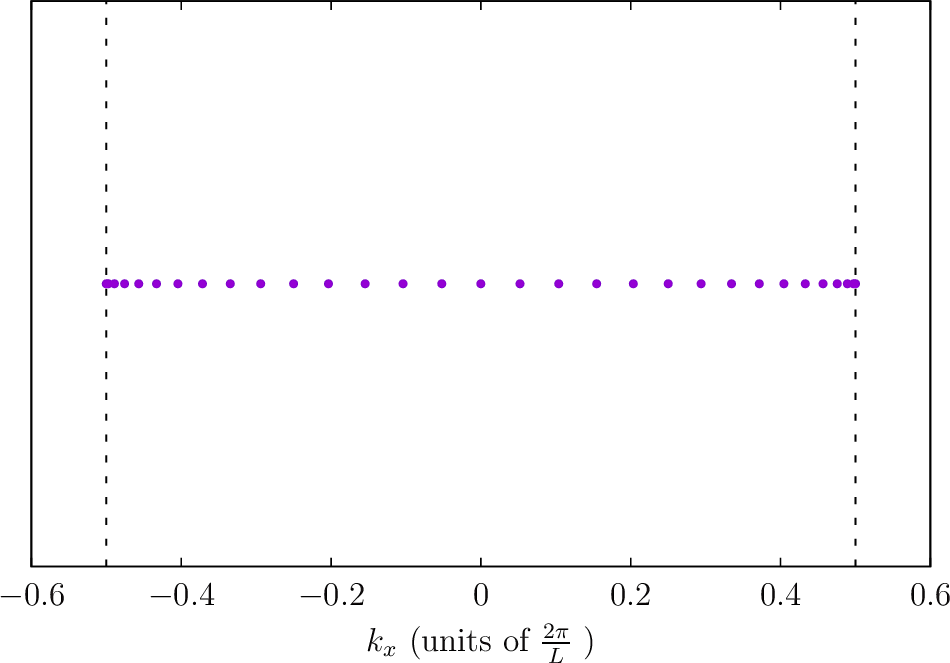
--BZIMethod CC    --BZIOrder  31    --BZSymmetryFactor 2

 

Comments