

Thermal radiation, heat transfer, and non-equilibrium Casimir forces between silicon dioxide spheres

In this example, we use scuff-neq to compute (1) the power radiated by a single SiO2 sphere, and (2) the heat transfer and non-equilibrium Casimir force between two SiO2 spheres. We compare the results of scuff-neq to the predictions of the T-matrix formalism of Krueger et al.

The files for this example may be found in the share/scuff-em/examples/SiO2Spheres subdirectory of your scuff-em installation.

---

gmsh geometry file and surface mesh for a single sphere

The gmsh geometry file Sphere.geo describes a sphere of radius 1 micron; it may be meshed to generate coarse and fine surface meshes as follows:

% gmsh -2 -clscale 1 Sphere.geo
% RenameMesh Sphere.msh
% gmsh -2 -clscale 0.5 Sphere.geo
% RenameMesh Sphere.msh

(Here RenameMesh is a simple bash script that uses scuff-analyze to count the number of interior edges in a surface mesh and rename the mesh file accordingly.) This produces the files Sphere_501.msh and Sphere_1479.msh, which you can visualize by opening in gmsh::

% gmsh Sphere_501.msh

% gmsh Sphere_1479.msh

---

scuff-em geometry files

The scuff-em geometry file SiO2Sphere_501.scuffgeo describes a single SiO2 sphere.

The scuff-em geometry files SiO2Spheres_501.scuffgeo SiO2Spheres_1479.scuffgeo each describe the same configuration: two SiO2 spheres separated by a center--center distance of 10 microns. You can visualize this configuration by typing e.g.

% scuff-analyze --geometry SiO2Spheres_1479.scuffgeo --WriteGMSHFiles
% gmsh SiO2Spheres_1479.pp

---

Spectral density of radiated power

As described in the scuff-neq documentation, scuff-neq computes temperature-independent quantities known as generalized fluxes, commonly denoted $\Phi(\omega)$, which describe the ability of systems to exchange energy and momentum via radiation at specific frequencies The total power radiated by a finite-temperature object is obtained as an integral over angular frequencies $\omega,$ in which the integrand involves a temperature-dependent Bose-Einstein factor and a temperature-independent dimensionless flux $\Phi.$ The distribution of labor in the scuff-em suite is that scuff-neq computes frequency-dependent generalized flux data and writes these in the form of data files, while a separate tool named scuff-integrate post-processes the flux data to yield temperature-dependent heat-transfer rates, powers, and torques.

To use scuff-neq to calculate radiated-power flux at a given set of frequencies, we say simply

 % scuff-neq --geometry SiO2Sphere_501.scuffgeo --OmegaFile MyOmegaFile

where MyOmegaFile is a list of angular frequencies.

This produces the file SiO2Sphere_501.SiFlux, which looks something like this:

# scuff-neq run on superhr2 (07/11/15::00:31:36)
# data file columns: 
# 1 transform tag
# 2 omega 
# 3 (sourceObject,destObject) 
# 4 PRad flux spectral density
DEFAULT 1.000000e-01 11 4.18911788e-06 
DEFAULT 1.300000e-01 11 1.38869207e-05 
DEFAULT 1.600000e-01 11 3.93335327e-05 
DEFAULT 1.900000e-01 11 1.05263974e-04 

As the file header says, the second column here is the angular frequency in units of $\omega_0=3\cdot 10^{14}$ rad/sec and the fourth column is the dimensionless power flux. (The first column lists the geometrical transformation; since we didn't specify the --transfile option to scuff-neq, we have just a single geometric configuration, labeled DEFAULT. The third column identifies the source and destination objects; since this geometry only has a single object, the source and destination object are both always object 1 and this column always reads 11.)

Here's a plot of the data:

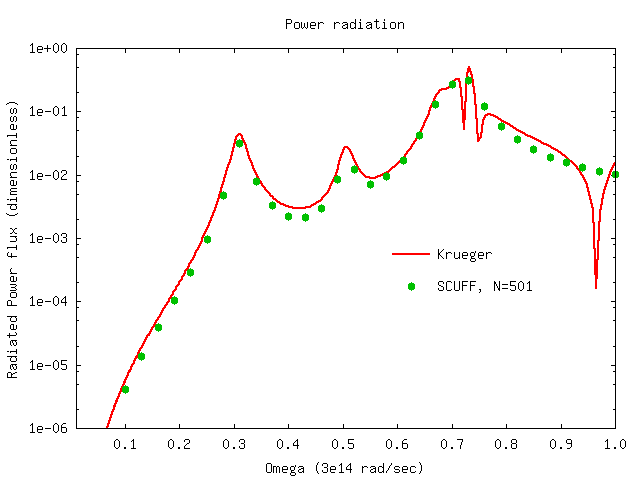
In this plot, the solid line is the prediction of the Krueger formalism, as computed by a julia code called KruegerFormulas.jl.

The plot is produced by gnuplot using this script.

---

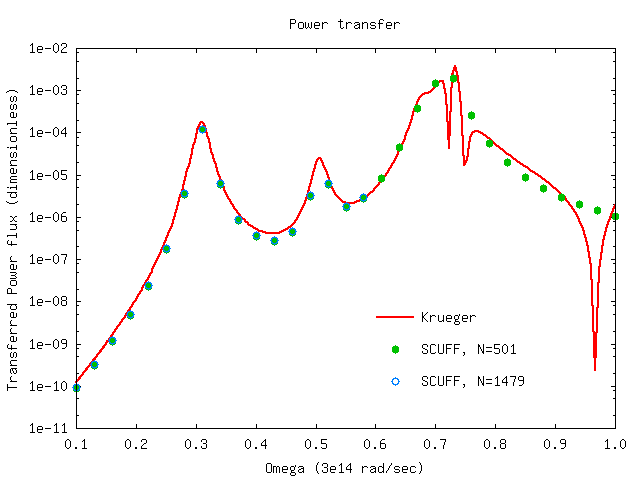
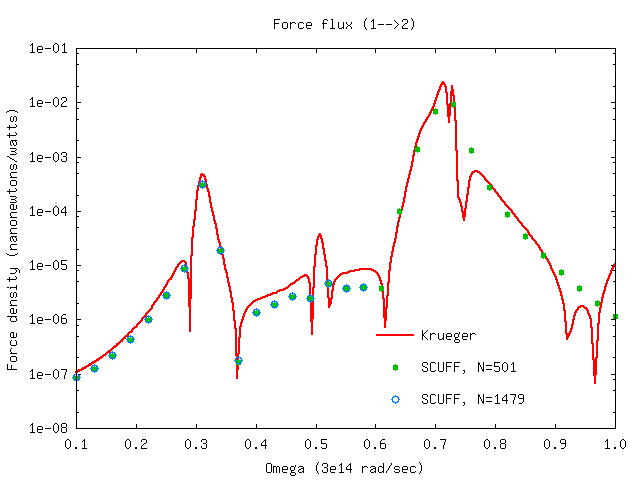
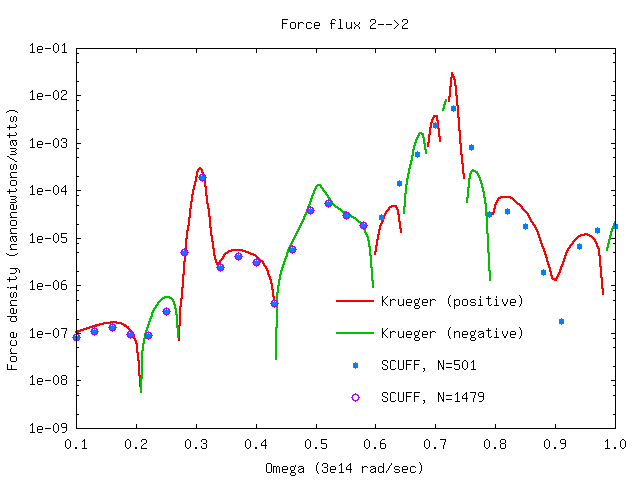
Spectral density of power transfer and non-equilibrium force

Here's a bash script that runs scuff-neq for both the coarsely-meshed and finely-meshed two-sphere geometry to compute the fluxes of power transfer and nonequilibrium force between the spheres. Running the script produces files SiO2Spheres_501.SIFlux and SiO2Spheres_1479.SIFlux. Here are plots (produced by the same gnuplot script referenced above) of the heat-transfer flux from sphere 1 to sphere 2, and the force fluxes from sphere 1 to sphere 2 and from sphere 2 to sphere 2, compared to the Krueger T-matrix results (again computed using the julia code referenced above).

---

Comments