

Computation of Singular Integrals in scuff-em

A key feature of scuff-em is an accurate and efficient code for computing singular four-dimensional integrals over pairs of triangles. The algorithm that scuff-em uses for this purpose---which I call the "generalized Taylor-Duffy method" in honor of the progenitors of some earlier methods that inspired it---is discussed in detail in this paper:

``Generalized Taylor–Duffy Method for Efficient Evaluation of Galerkin Integrals in Boundary-Element Method Computations'', IEEE Transactions on Antennas and Propagation 63 195 (2015).

DOI: 10.1109/TAP.2014.2367492

ArXiV: http://arxiv.org/abs/1312.1703.

The code that evaluates singular integrals is packaged with the scuff-em distribution; it is contained in a single C++ file named TaylorDuffy.cc (around 1,500 lines). This code calls the pcubature code from Steven G. Johnson's numerical cubature package.

Also, here are the mathematica codes mentioned in the paper above:

This page is intended for developers who would like to use the scuff-em implementation of the generalized Taylor-Duffy method in their own codes.

Table of Contents

1. What the code actually computes
2. C++ calling convention
3. Simple demonstration program

1. What the code actually computes

The code provides a C++ function named TaylorDuffy which computes the following four-dimensional integral over a triangle-product domain: $\mathcal{I}= \frac{1}{4AA^\prime} \int_{\mathcal T} \, d\mathbf x \, \int_{\mathcal T^\prime} \, d\mathbf x^\prime \, P\big(\mathbf x, \mathbf x^\prime\big) K\big(|\mathbf x-\mathbf x^\prime|\big) \qquad (1)$

In this expression,

$\mathcal T$ and $\mathcal T^\prime$ are triangles with at least one common vertex. (You supply to TaylorDuffy the cartesian coordinates of the triangle vertices.)

P is a polynomial function of 6 variables (the Cartesian components of x,x'). Although the underlying algorithm works for arbitrary polynomials P, in the implementation of TaylorDuffy provided below you will select one of a predetermined set of possible polynomials (see below). Modifying the code to support other polynomials would be a relatively straightforward, if tedious, task.

K is a kernel function of a single scalar variable r. Although the algorithm works for a fairly wide family of kernel functions, in the implementation of TaylorDuffy provided below you will select one of a predetermined set of possible kernels (see below). Again, it should be relatively straightforward to modify the code to support other kernels.

Actually, it is more accurate to say that TaylorDuffy computes multiple simultaneous integrals of the form (1); in a single call to TaylorDuffy you can specify, for the same triangle pair T,T', more than one (polynomial, kernel) pair, i.e. {P_n, K_n} for n=1,2,...,N, and TaylorDuffy will compute all N integrals at once. This is faster than making N separate calls due to the reuse of computational overhead.

2. C++ calling convention

The TaylorDuffy routine has many input arguments (many of which may be set to default values) and multiple output values. For this reason, instead of the typical calling convention in which you specify multiple input arguments to a C++ function and get back a single output value, TaylorDuffy accepts as its argument a (pointer to a) single big argument structure.

Thus, within a C/C++ program, to evaluate one or more integrals of the form (1) for a given pair of triangles you will

instantiate and initialize a data structure of type TaylorDuffyArgStruct, which stores all input and output arguments, and then
simply call TaylorDuffy() with a pointer to your argument structure as the only parameter. On return, the results (the values of the integral) will be stored in the argument structure.

The process looks like this:

 // instantiate and initialize argument structure 
 TaylorDuffyArgStruct MyTDArgs, *TDArgs=&MyTDArgs;
 InitTaylorDuffyArgs(TDArgs); // always call this!

 // fill in necessary fields 
 TDArgs->WhichCase = TD_COMMONVERTEX
 TDArgs->NumPKs    = 1; 
 ...

 // evaluate the integral
 TaylorDuffy(TDArgs);

 // results are now available inside TDArgs
 printf("Result: %e \n", real(TDArgs->Result[0]) );

Thread Safety

TaylorDuffy() is thread-safe; you may call it from multiple simultaneously-executing threads without fear of crosstalk or race conditions. (Indeed, scuff-em does just this if compiled with support for openmp or pthreads.)

Fields in `TaylorDuffyArgStruct`

The table below details all fields in the argument structure passed to TaylorDuffy.

In general, you should always call InitTaylorDuffyArgs first to set all optional fields to default values, then fill in your desired values for mandatory fields (and overwrite the default values for any optional fields you wish to tweak).

Field Description

Mandatory input fields describing the triangles

int WhichCase; Counts the number of common vertices between the two triangles. You should set this to 1, 2, or 3 for the common-vertex, common-edge, or common-triangle cases. (The file TaylorDuffy.h defines the constants TD_COMMONVERTEX=1, TD_COMMONEDGE=2, TD_COMMONTRIANGLE=3).

double *V1, *V2, *V3;

double *V2P, *V3P;

Pointers to caller-allocated arrays of length 3 containing the x,y,z coordinates of the triangle vertices.

V1, V2, V3 are the vertices of triangle T. For example, V2[0,1,2] are the x,y,z coordinates of the second vertex.

V2P, V3P are the vertices of triangle T' that are not shared with triangle T. It is not always necessary to initialize these fields. In particular,

In the common-triangle case (WhichCase=3), neither V2P nor V3P is referenced.
In the common-edge case (WhichCase=2), only V3P is referenced; V2P is ignored.
In the common-vertex case (WhichCase=1), both V2P and V3P are referenced.

Mandatory input fields describing the P and K functions

int NumPKs;

int *PIndex;

int *KIndex;

int *KParam;

NumPKs specifies the number of integrals of the form (1) you wish to compute (that is, the number of pairings of a polynomial P with a kernel K) for the given pair of triangles. If you only need to compute a single integral, set NumPKs=1.

PIndex and KIndex are pointers to caller-allocated arrays of length NumPKs. The nth entries in these arrays are the indices (in the tables below) of the nth P and K functions.

KParam is a pointer to a caller-allocated array of length NumPKs containing values of certain parameters that enter the kernel functions. The entries of this array are interpreted in different ways depending on the corresponding entries in the KIndex array:

If KIndex[n]==TD_RP (the r^p kernel), then KParam[n] is interpreted as the parameter p, i.e. the integer power to which r is raised. (The cdouble-valued quantity KParam[n] is converted to int inside TaylorDuffy.)
For all other kernels, KParam[n] is interpreted as the parameter k, i.e. the Helmholtz wavenumber. This quantity can be purely real, purely imaginary, or complex.

Input fields that are required for certain P functions

double *Q, *QP; Pointers to caller-allocated arrays of length 3 containing the x,y,z coordinates of the RWG source/sink vertices Q,Q'. These are only referenced if any entry in the PIndex array corresponds to one of the polynomials in the table below whose definition involves Q,Q'.

double *nHat; Pointers to caller-allocated arrays of length 3 containing the x,y,z components of the unit normal vector n. This is only referenced if any entry in the PIndex array corresponds to one of the polynomials in the table below whose definition involves n.

Optional input fields controlling integration behavior

double AbsTol, RelTol; The absolute and relative error tolerances to which the adaptive integrator will attempt to compute the integral. (The defaults are AbsTol=0.0 and RelTol=1.0e-10.)

int MaxEval; An upper bound on the number of function samples the adaptive integrator may compute. (The default is MaxEval=1000.) Reducing this number will cause the code to run more quickly, possibly at the expense of lower accuracy.

Output fields

cdouble *Result, *Error; Pointers to caller-allocated output buffers with enough space to store NumPKs values of type cdouble. On return, Result[n] is the value of the integral for the nth P,K pairing, and Error[n] is an estimate of the error incurred by the numerical quadrature.

int nCalls; The number of function evaluations used to evaluate the numerical cubature. This number will not exceed MaxEval.

Values of the `PIndex` field

The implementation of TaylorDuffy provided here contains support for the following choices of the P polynomial in equation (1). (The values of the PIndex field here are constants defined in TaylorDuffy.h.)

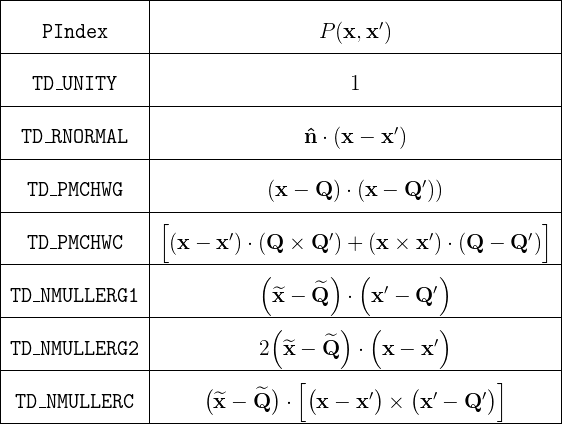
P index table

In this table, the quantities Q, Q', n are vector-valued parameters that you specify by setting fields in the argument structure for the TaylorDuffy routine (see above). Also, in the final three table entries, the tilde symbol above a vector-valued quantity indicates the result of crossing that quantity with the normal vector you specify via the nHat field in the argument structure (see above):

$\widetilde{\mathbf x} \equiv \mathbf{\hat n} \times \mathbf x, \qquad \widetide{\mathbf Q} \equiv \mathbf{\hat n} \times \mathbf Q$

For RWG basis-function enthusiasts, note that the last 5 entries in the table are appropriate for computing matrix elements of the EFIE and MFIE operators between RWG basis functions, but observe carefully that the prefactor $\frac{1}{4AA'}$ in the definition (1) is only part of the full prefactor that arises for RWG basis functions; there is also a factor ll' (product of edge lengths) which is missing from these calculations, and you must put that in yourself, by hand.

Values of the `KIndex` field

The implementation of TaylorDuffy provided here contains support for the following choices of the K kernel in equation (1). (The values of the KIndex field here are constants defined in TaylorDuffy.h.)

K index table

In this table, the values of the parameters p and k are what you put into the KParam array in the TaylorDuffyArgStruct.

3. Simple demonstration program

Here is a little test program that you can download and compile against the scuff-em core library to test the code:

TestTaylorDuffy.cc

Sample output:

% TestTaylorDuffy 
Integrand sampled at 33 points.
Integral 1: +3.56771698e-01  (estimated error: 6.0e-12)
Integral 2: +1.57003236e-03  (estimated error: 1.2e-11)
Computation time: 1.209307e+02 microseconds

Here is a listing of the program:

#include "TaylorDuffy.h"
using namespace scuff;

int main(int argc, char *argv[])
{
  /* panel vertices */
  int WhichCase = 2; // 2 common vertices
  double V1[3]  =  { 0.0,  0.0,  0.0 };
  double V2[3]  =  { 0.1,  0.0,  0.0 };
  double V3[3]  =  { 0.05, 0.1,  0.0 };
  double V3P[3] =  { 0.07, -0.08, 0.03 };

  double *Q     = V3;  // source/sink vertex, triangle 1
  double *QP    = V3P; // source/sink vertex, triangle 2

  /* specification of which integrals we want */
  int NumPKs        = 2;
  int PIndex[2]     = {TD_UNITY, TD_PMCHWC};
  int KIndex[2]     = {TD_RP,    TD_RP};
  cdouble KParam[2] = {-1.0,    -3.0};

  /* output buffers */
  cdouble Result[2], Error[2];

  /* fill in argument structure with problem description */
  TaylorDuffyArgStruct MyTDArgs, *TDArgs=&MyTDArgs;
  InitTaylorDuffyArgs(TDArgs);
  TDArgs->WhichCase = WhichCase;
  TDArgs->V1        = V1;
  TDArgs->V2        = V2;
  TDArgs->V3        = V3;
  TDArgs->V3P       = V3P;
  TDArgs->Q         = Q;
  TDArgs->QP        = QP;
  TDArgs->NumPKs    = NumPKs;
  TDArgs->PIndex    = PIndex;
  TDArgs->KIndex    = KIndex;
  TDArgs->KParam    = KParam;
  TDArgs->Result    = Result;
  TDArgs->Error     = Error;  

  /* specify desired error tolerance */
  TDArgs->RelTol    = 1.0e-10;   // request 10-digit accuracy
  TDArgs->MaxEval   = 25;        // upper limit on integrand samples

  /* calculate the integral */
  TaylorDuffy( TDArgs );

  /* print the results */
  printf("Integrand sampled at %i points.\n",TDArgs->nCalls);
  printf("Integral 1: {%+.8e, %+.8e} (estimated error {%.1e.,%.1e}) \n",
          real(Result[0]),imag(Result[0]),real(Error[0]),imag(Error[0]));
  printf("Integral 2: {%+.8e, %+.8e} (estimated error {%.1e.,%.1e}) \n",
          real(Result[1]),imag(Result[1]),real(Error[1]),imag(Error[1]));

  /* uncomment the following line to report computation time */
//#define MEASURE_RUNTIME
#ifdef MEASURE_RUNTIME
#define REPETITIONS 100
  Tic();
  for(int n=0; n<REPETITIONS; n++)
   TaylorDuffy( TDArgs );
  double TimeElapsed = Toc() / REPETITIONS;
  printf("Computation time: %e microseconds\n",1.0e6*TimeElapsed);
#endif

}

And here is a simple Makefile that compiles and links against the scuff-em installation on your system (you'll need to modify a few lines at the top of this file appropriately for your system):

# top of SCUFF-EM src tree
SCUFF_SRC=$(HOME)/work/scuff-em

# SCUFF-EM installation prefix (set with --prefix when running configure)
SCUFF_INSTALL=$(HOME)/work/scuff-em-installation

# HDF5 / Lapack libraries
HDF5_LIBS=-lhdf5_hl -lhdf5
MATH_LIBS=-lopenblas -lgomp -lgfortran -lpthread

##################################################
# shouldn't need to modify the rest
##################################################
CPPFLAGS+=-I$(SCUFF_SRC)/libs/libscuff 
CPPFLAGS+=-I$(SCUFF_INSTALL)/include/scuff-em

LIBDIR=$(SCUFF_INSTALL)/lib
LDFLAGS+=-L$(LIBDIR) -Wl,-rpath,$(LIBDIR)

SCUFF_LIBS=-lscuff
LIBS=$(SCUFF_LIBS) $(HDF5_LIBS) $(MATH_LIBS)

TestTaylorDuffy:        TestTaylorDuffy.o
                $(CXX) $(LDFLAGS) -o $@ $^ $(LIBS)

Computation of Singular Integrals in scuff-em

1. What the code actually computes

2. C++ calling convention

Thread Safety

Fields in TaylorDuffyArgStruct

Values of the PIndex field

Values of the KIndex field

3. Simple demonstration program

Comments

Fields in `TaylorDuffyArgStruct`

Values of the `PIndex` field

Values of the `KIndex` field