

Capacitance of parallel-plate and two-sphere capacitors

In this example, we exploit scuff-em's electrostatics module to compute the capacitance of parallel-plate and two-sphere capacitors.

The files for this example may be found in the share/scuff-em/examples/TwoBodyCapacitors subdirectory of your scuff-em installation.

Capacitance of a parallel-plate capacitor

I consider a parallel-plate capacitor consisting of two square conducting plates of side length $L$ separated by various distances $d$ . Neglecting fringing-field (i.e. finite-size) effects, the capacitance is $C(d)=\epsilon_0 \frac{L^2}{d}.$

Creating scuff-em input files

Because electrostatics is scale-invariant, I can choose length units arbitrarily, and I will choose units in which $L=1$ . To specify my geometry thus requires meshed representations of squares of side length 1, which I generate (at two different meshing resolutions) like this in gmsh:

% gmsh -setnumber N 10 -2 Square_N.geo -o Square.msh 
% RenameMesh Square.msh
% gmsh -setnumber N 20 -2 Square_N.geo -o Square.msh 
% RenameMesh Square.msh

Here Square_N.geo is the gmsh input file and RenameMesh is a little script that uses [scuff-analyze][scuff-analyze] to count the number of interior edges in a surface mesh and rename the file accordingly.

This produces files named Square_280.msh and Square_1160.msh. Now write scuff-em geometry files:

+TwoPlateCapacitor_280.scuffgeo

+TwoPlateCapacitor_1160.scuffgeo

and a list of geometrical transformations describing 20 values of the plate-plate spacing $d$ ranging from $d=0.01L$ to $d=L$ :

+TwoPlateCapacitor.trans

Before running calculations, double-check that our .scuffgeo and .trans files file correctly describe the range of geometries we want to study:

% scuff-analyze --geometry TwoPlateCapacitor_280.scuffgeo --transfile TwoPlateCapacitor.trans 
% gmsh TwoPlateCapacitor_280.transformed.pp

Running the calculation

% for N in 280 1160
% do
%   ARGS=""
%   ARGS="${ARGS} --geometry  TwoPlateCapacitor_${N}.scuffgeo"
%   ARGS="${ARGS} --TransFile TwoPlateCapacitor.trans"
%   ARGS="${ARGS} --CapFile   TwoPlateCapacitor_${N}.out"
%   scuff-static ${ARGS}
% done

Plotting the data

% gnuplot
gnuplot> set logscale xy
gnuplot> plot 'TwoPlateCapacitor_280.out' u 1:(abs($3)) t 'SCUFF, N=280' w p pt 7 ps 1, 'TwoPlateCapacitor_1160.out' u 1:(abs($3)) t 'SCUFF, N=1160' w p pt 6 ps 2, 1/x w l lw 2 t 'Theoretical Prediction'

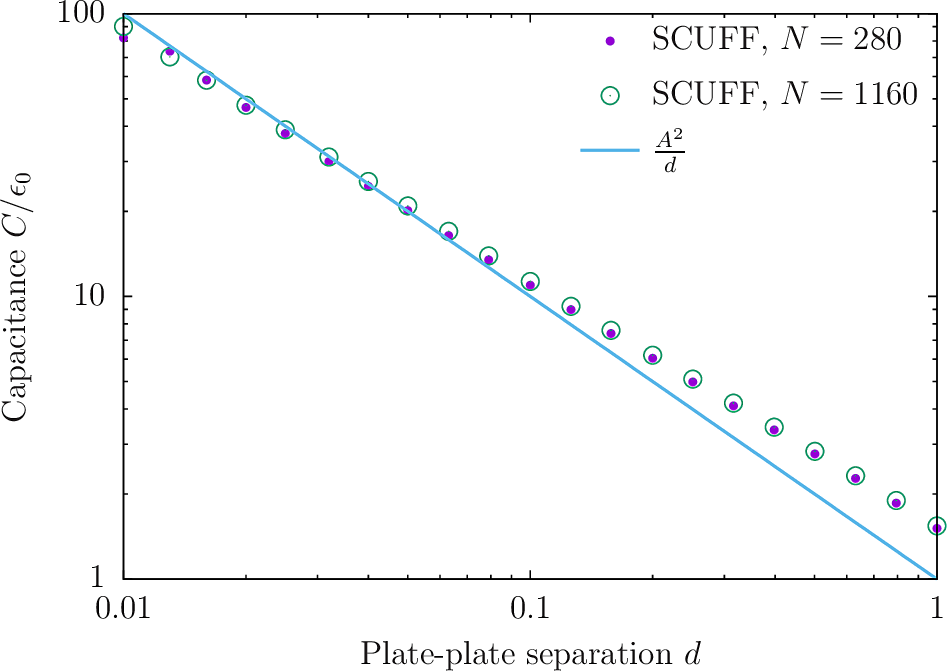
The deviations from the theoretical prediction at small $d$ are due to finite mesh resolution and are reduced in the finer-mesh calculation. On the other hand, the deviations at large $d$ are due to the finite size of the plates and are not changed by computing at finer resolution.

Capacitance of a two-sphere capacitor

The share/scuff-em/examples/TwoBodyCapacitors subdirectory of your scuff-em installation also contains input files for computing the self- and mutual capacitances of a capacitor consisting of two conducting spheres of radius $R$ separated by a surface-surface separation distance $d$ (center-center separation $d+2R$ ). Analytical formulas for the self-capacitance $C_{11}=C_{22}$ and mutual capacitance $C_{12}=C_{21}$ for this case may be found in this paper from 1926:

A. Russell, "The problem of the spherical condenser", Journal of the Institution of Electrical Engineers 64 727 (1926). DOI: 10.1049/jiee-1.1926.0065

The scuff-static computation proceeds as above with new geometry and transformation files:

% for N in 501 2604
% do
%   ARGS=""
%   ARGS="${ARGS} --geometry  TwoSphereCapacitor_${N}.scuffgeo"
%   ARGS="${ARGS} --TransFile TwoSphereCapacitor.trans"
%   ARGS="${ARGS} --CapFile   TwoSphereCapacitor_${N}.out"
%   scuff-static ${ARGS}
% done

This time we'll plot both $C_{11}(d)$ and $C_{12}(d)$ and compare against the large- $d$ and small- $d$ analytical formulas in the paper of Russel above.

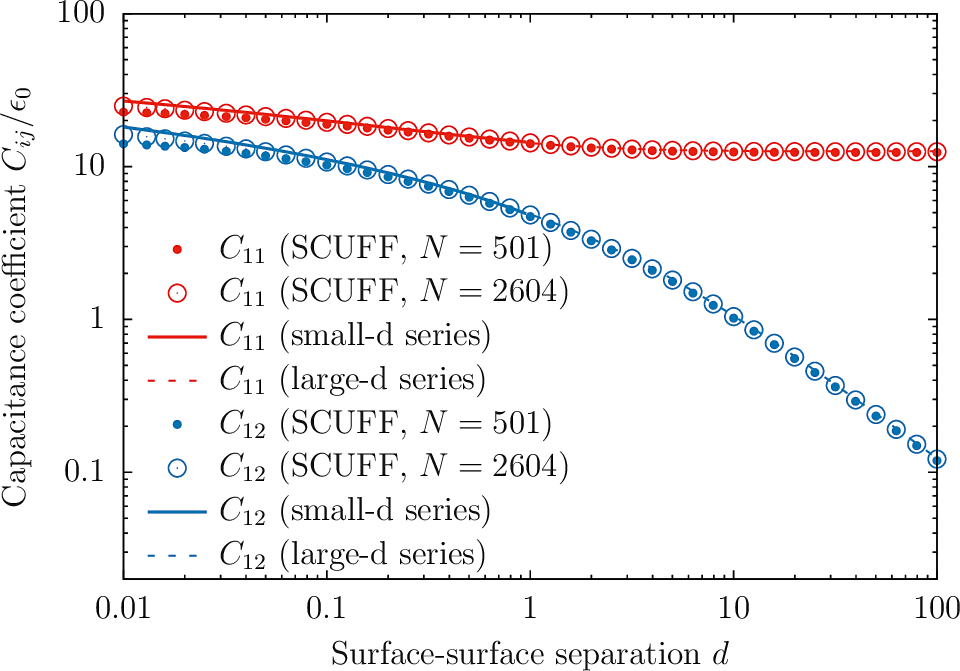
Here's the gnuplot script I used to make this plot: TwoSphereCapacitor.gp.