

Equilibrium Casimir forces between spheres

This test validates the scuff-cas3d of the scuff-em code suite by using it to compute the equilibrium Casimir force between identical spheres at various separation distances. We consider both perfectly electrically conducting (PEC) and dielectric spheres.

Analytical solution

An analytical formula for the distance-dependent Casimir energy of two identical PEC spheres of radius $R$ separated by a distance $d$ was obtained by T. Emig et al. in this paper:

• T. Emig, N. Graham, R. L. Jaffe, and M. Kardar, "Casimir forces between arbitrary compact objects." Physical Review Letters 99 170403 (2007).

Their asymptotic ($d\gg R$) formula for the energy, and the force formula obtained by differentiating it, are

$$E(d) = -\frac{\hbar c}{\pi R} \sum_{n=7}^\infty C_n \left(\frac{R}{d}\right)^n$$ $$F(d) = -\frac{\hbar c}{\pi R^2} \sum_{n=7}^\infty n C_n \left(\frac{R}{d}\right)^{n+1}$$

where the first few $C$ coefficients are

• for PEC spheres: $$C_7=\frac{143}{16}, \quad C_9=\frac{7947}{160}, \quad C_{10}=\frac{2065}{32}$$

• for dielectric spheres with static $(\omega \to 0)$ relative permittivity $\epsilon$: $$C_7=\frac{23}{4}\left(\frac{\epsilon-1}{\epsilon+2}\right)^2$$

scuff-em solution

The Casimir energy and force between two PEC spheres and between two dielectric spheres may be computed using scuff-cas3d as follows:

 % scuff-cas3d --geometry PECSpheres_501.scuffgeo --translist Spheres.trans --energy --zforce
 % scuff-cas3d --geometry E10Spheres_501.scuffgeo --translist Spheres.trans --energy --zforce

Here the two .scuffgeo files (PECSpheres_501.scuffgeo and E10Spheres_501.scuffgeo] describe the two geometric configurations (two PEC spheres and two dielectric spheres of radius $R=1\, \mu$m separated by an initial center-center distance of $d$=3 $\mu$m) while Spheres.trans specifies the list of center-center separation distances $d$ at which we compute the energy and force. (Both geometries refer to the same surface mesh file for the sphere, Sphere_327.msh.

The above calculations produce output files named PECSpheres_327.out and E10Spheres_327.out. Plotting against the theoretical predictions of Emig et. al (referenced above) yields good agreement:

.

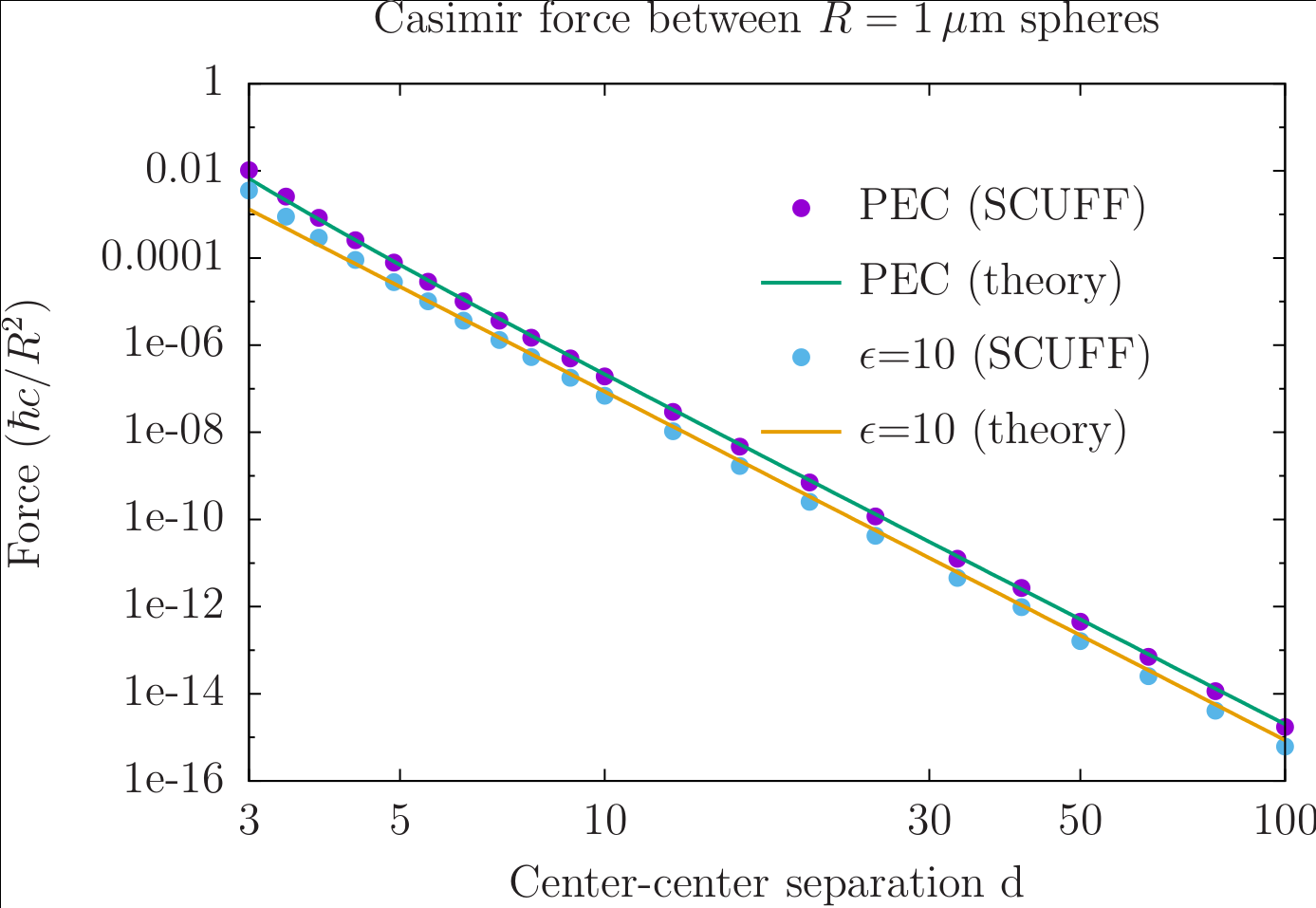Here's the gnuplot script I used to produce this plot: Plotter.gp.

Comments