

Fresnel Scattering

The FresnelScattering unit of the scuff-em test suite uses the scuff-transmission command-line module to study the textbook case of Fresnel scattering: the transmission and reflection of plane waves at a planar dielectric interface of infinite extent in the transverse dimensions.

More specifically, we consider plane waves incident from below on a dielectric half-space of permittivity $\epsilon_r=10.$ The geometry is 2D-periodic with a unit cell of dimensions $L_x=L_y=1\, \mu$ m; the only meshed surface is the planar interface between vacuum ( $z<0$ ) and dielectric ( $z>0$ ), described by a mesh with 40 interior edges. The incident angle of the plane wave determines the Bloch vector of the scattering problem.

The aspects of scuff-em functionality exercised by this test include the following:

Core library (libscuff)

Basic handling of periodic geometries. Parsing of LATTICE...ENDLATTICE statements in .scuffgeo files. Processing of "straddler" basis functions in periodic geometries containing surfaces that extend across unit-cell boundaries. (libscuff/PBCSetup.cc)
Computation of 2D periodic Green's function via Ewald summation (GBarVDEwald.cc) and its acceleration via interpolation table (GBarAccelerator.cc)
Assembly of system matrix for 2D Bloch-periodic geometries, including acceleration scheme involving separating contributions of innermost 9 cells from contributions of outer ("all but inner" or ABI) cells (AssembleBEMMatrix.cc).
Computation of scattered fields for Bloch-periodic geometries (GetFields.cc).

libmdinterp support library:

Instantiation and use of 2D and 3D interpolation tables (Interp2D.cc, Interp3D.cc)

scuff-transmission command-line application module:

Computation of transmission and reflection coefficients directly from surface currents (GetAmplitudes.cc)
Computation of transmitted and reflected power via Poynting-vector integration using scattered fields (GetFlux.cc)

Exact solution

The situation considered here is that of a plane wave impinging from below on a dielectric half-space (relative permittivity $\epsilon=10$ ) filling the region $z>0$ . (More details on the setup for scuff-transmission calculations may be found in the document Computation of reflection and transmission coefficients in scuff-em.)

For this case, the transmission and reflection coefficients for the TE and TM polarizations read

$t^{\scriptsize{\text{TE}}} =\frac{2\cos\theta}{\cos\theta + \cos\theta^\prime}, \qquad r^{\scriptsize{\text{TE}}} =\frac{\cos\theta-\cos\theta^\prime}{\cos\theta + \cos\theta^\prime},$ $t^{\scriptsize{\text{TM}}} =\frac{2n\cos\theta}{n^2 \cos\theta + \cos\theta^\prime}, \qquad r^{\scriptsize{\text{TM}}} =\frac{n^2\cos\theta-\cos\theta^\prime}{n^2\cos\theta + \cos\theta^\prime}$

where $\theta$ is the incident angle ( $\theta=0$ for normal incidence), $n=\sqrt{\epsilon}$ is the index of refraction, and

$\cos\theta^\prime = \sqrt{ \epsilon - \sin^2\theta}.$

scuff-em solution

The transmission and reflection coefficients for the $\epsilon=10$ dielectric half-space problem are computed using scuff-transmission as follows:

ARGS=""
ARGS="${ARGS} --geometry    E10HalfSpace_40.scuffgeo"
ARGS="${ARGS} --Omega       0.1"
ARGS="${ARGS} --Omega       1.0"
ARGS="${ARGS} --ThetaMin    0"
ARGS="${ARGS} --ThetaMax    85"
ARGS="${ARGS} --ThetaPoints 19"
ARGS="${ARGS} --ZAbove      1.0"
 % scuff-transmission ${ARGS}

Here the file E10HalfSpace_40.scuffgeo describes the scuff-em geometry (it refers to a mesh file named Square_40.msh ) and the command-line arguments ask for a calculation at two angular frequencies ( $\omega=\{0.1, 1\}\omega_0$ with $\omega_0\equiv 3\times 10^{14}$ rad/sec the default unit of angular frequency) and at 20 incident angles in the range $0\le \theta < 90$ degrees.

Comparison

Running the above command yields the file E10HalfSpace_40.transmission. Plotting in gnuplot yields a comparison of scuff-transmission data (point) to theoretical predictions (curves):

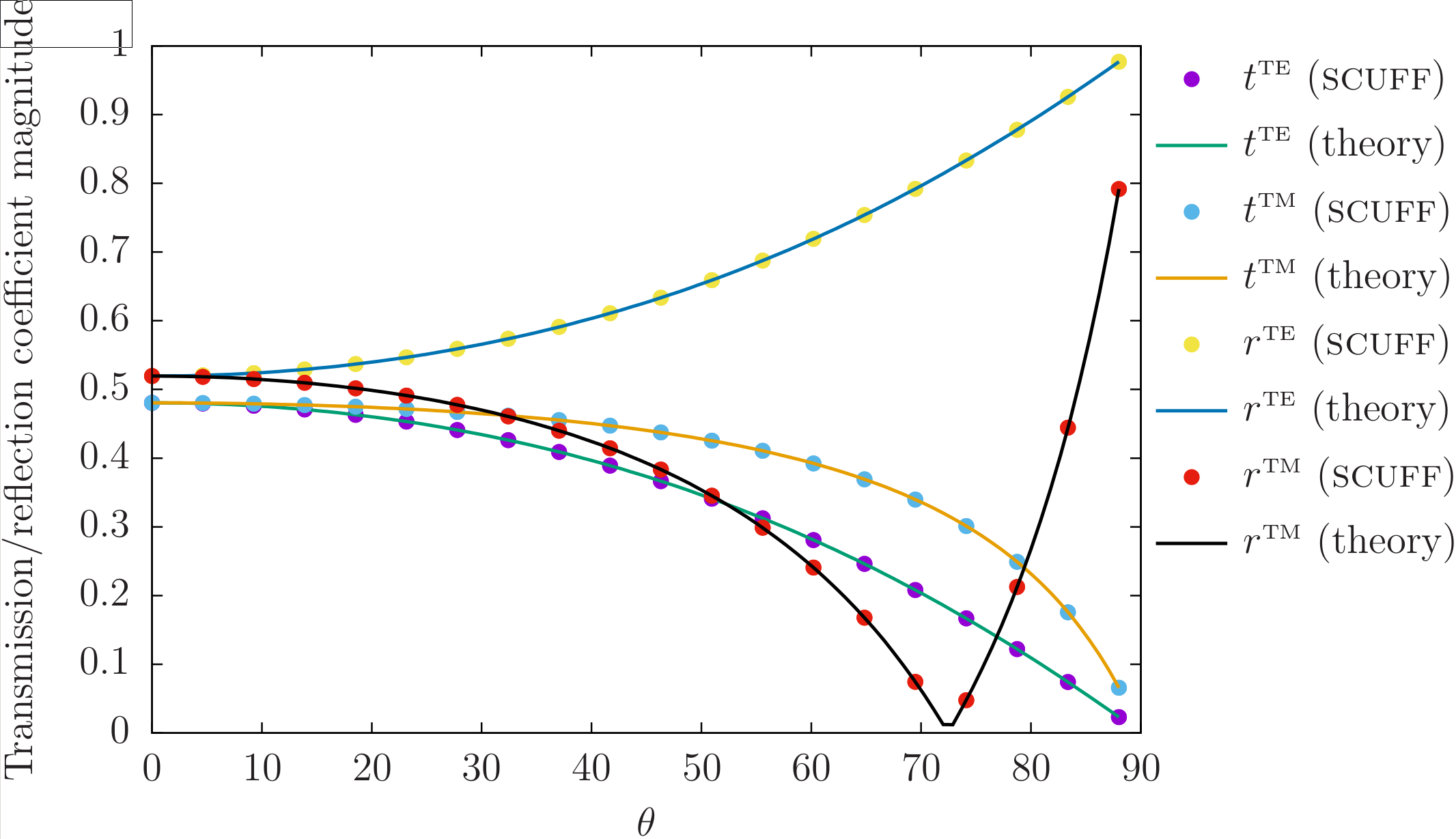
Here is the gnuplot script that I use to produce this plot: PlotFresnelData.gp.

Unit test

The unit test is performed by running the script tests/Fresnel/TestFresnel.sh. This runs scuff-transmission to do the calculation described above, with results written to output file E10HalfSpace_40.transmission. The CheckSCUFFData utility is then invoked to compare the content of this file against the reference file E10HalfSpace_40.transmission.reference. (To generate this reference file, run % TestFresnel.sh --reference with no other arguments.) The items to be checked in the comparison are defined by the checklist Fresnel.Checklist. The unit test passes iff all data items for all data sets agree within specified tolerances.